笛卡儿轨迹规划策略优化

在这种轨迹规划系统中，作业是用机械手终端位姿的笛卡儿坐标节点序列规定的。因此，节点指的是表示机械手终端位姿（位置和姿态）的齐次变换矩阵。

1.物体对象的描述

利用第3章有关物体空间的描述方法，任一刚体相对参考系的位姿是用与它固接的坐标系来描述的。相对于固接坐标系，物体上任一点用相应的位置矢量p表示，任一方向用方向余弦表示。给出物体的几何图形及固接坐标系后，只要规定固接坐标系的位姿，即可重构该物体。

例如，图6-5所示的螺栓，其轴线与固接坐标系的z轴重合。螺栓头部直径为32 mm，其中心取为坐标原点，螺栓长80 mm，螺栓杆直径为20 mm，则可根据固接坐标系的位姿重构螺栓在空间（相对于参考坐标系）的位姿和几何形状。

2.作业的描述

作业和机械手的运动可用手部位姿节点序列来规定，每个节点由工具坐标系相对于作业坐标系的齐次变换矩阵来描述。相应的关节变量可用运动学反解程序计算。

例如，要求机器人按直线运动，把螺栓从槽中取出并放入托架的一个孔中，如图6-6所示。

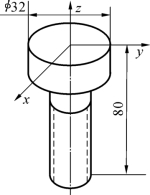
图6-5　对象的描述

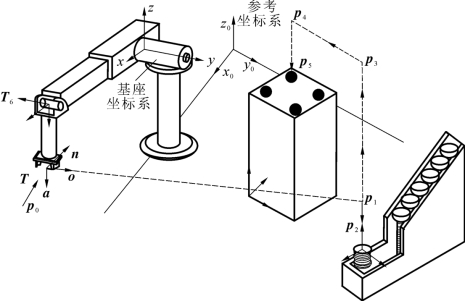
图6-6　作业的描述

用符号表示沿直线运动的各节点的位姿，使机器人能沿虚线运动并完成作业。令pi（i=0，1，2，3，4，5）为夹手必须经过的直角坐标节点。参照这些节点的位姿将作业描述为如表6-2所示的手部的一连串运动和动作。

表6-2　手部对螺栓的抓取和插入过程

每一节点pi对应一个变换方程，从而解出相应的机械手的变换矩阵0T6。由此得到作业描述的基本结构：作业节点pi对应机械手变换矩阵0T6，从一个节点变换到另一个节点通过机械手运动实现。

3.两个节点之间的“直线”运动

机械手在完成作业时，夹手的位姿可用一系列节点pi来表示。因此，在直角坐标空间中进行轨迹规划的首要问题是，如何在分别由两节点pi和pi+1所定义的路径起点和终点之间，生成一系列中间点。两节点之间最简单的运动是在空间的直线移动和绕某定轴的转动。若运动时间给定，则可以产生一个使线速度和角速度受控的运动。如图6-7所示，要生成从节点p0（原位）运动到pi（接近螺栓）的轨迹。更一般地，从节点pi到下一节点pi+1的运动可表示为从

到

的运动。其中，6TE是工具坐标系｛T｝相对末端连杆系｛6｝的变换。Bpi和Bpi+1分别为两节点pi和pi+1相对坐标系｛B｝的齐次变换。如果起始点pi是相对于另一坐标系｛A｝描述的，那么可通过变换过程得到

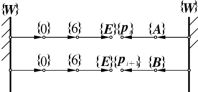
图6-7　两节点之间的运动变换

基于式（6-24）和式（6-25），则从节点pi到pi+1的运动可由驱动变换函数D（λ）来表示：

式中：驱动变换D（λ）是归一化时间λ的函数；λ=t/T，λ∈[0，1]，其中t为自运动开始算起的实际时间，T为走过该轨迹段的总时间。

在节点p，实际时间t=0，因此λ=0，D（0）是4×4的单位矩阵，因而式（6-27）与式（6-24）相同。

在节点pi+1，t=T，λ=1，有

因此得

可将工具（机器人末端）从一个节点pi到下一节点pi+1的运动看成和机器人末端固接的坐标系的运动。在第3章中，规定手部坐标系的三个坐标轴用n，o和a表示，坐标原点用p表示。因此，节点pi和pi+1相对于目标坐标系｛B｝的描述可用相应的齐次变换矩阵来表示，即

式中：n˙o——矢量n与o的标量积。

工具坐标系从节点pi到pi+1的运动可分解为一个平移运动和两个旋转运动：第一个转动使工具轴线与预期的接近方向a对准；第二个转动是绕工具轴线（a）的转动，对准方向矢量o。则驱动函数D（λ）由一个平移运动和两个旋转运动构成，即(www.xing528.com)

式中：L（λ）——平移运动的齐次变换，其作用是把节点pi的坐标原点沿直线运动到pi+1的坐标原点；

Ra（λ）——第一个转动的齐次变换，其作用是将pi的接近矢量ai转向pi+1的接近矢量ai+1；

Ro（λ）——第二个转动的齐次变换，其作用是将pi的方向矢量oi转向pi+1的方向矢量oi+1。

L（λ），Ra（λ），Ro（λ）分别为

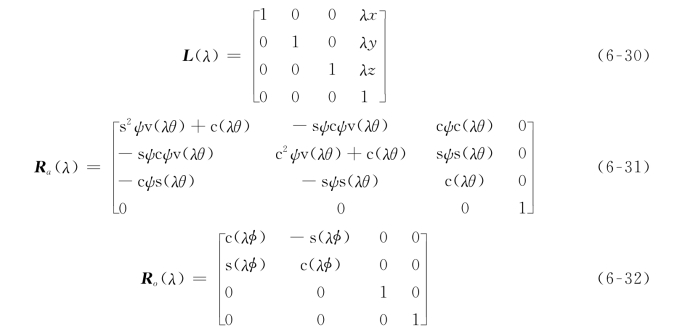
式中：sψ=sinψ；cψ=cosψ；v（λθ）=Vers（λθ）=1-cos（λθ）；c（λθ）=cos（λθ）；s（λθ）=sin（λθ）；c（λφ）=cos（λφ）；s（λφ）=sin（λφ）；λ∈[0，1]。

旋转变换Ra（λ）表示绕矢量k转动θ角得到的变换矩阵，而矢量k是pi的y轴绕其z轴转过ψ角得到的，即

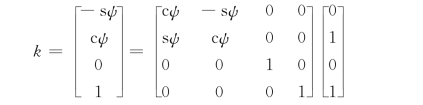
根据旋转变换通式，即可得到式（6-32）。旋转变换Ra（λ）表示绕接近矢量a转φ角的变换矩阵。显然，平移量λx，λy，λz和转动量λθ及λφ将与λ成正比。若λ随时间线性变化，则D（λ）所代表的合成运动将是一个恒速移动和两个恒速转动的复合。

将矩阵（6-30）至矩阵（6-32）相乘代入式（6-29），得到

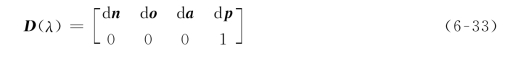
式中：

4.两段路径之间的过渡

前面利用驱动变换D（λ）来控制一个移动和两个转动生成两节点之间的“直线”运动轨迹0T6（λ）=0TBBpiD（λ）6T-1E，现在讨论两段路径之间的过渡问题。为了避免两段路径衔接点处速度不连续，当由一段轨迹过渡到下一段轨迹时，需要加速或减速。在机械手终端到达节点前的时刻τ开始改变速度，然后保持加速度不变，直至到达节点之后τ（单位时间）为止，如图6-8所示。

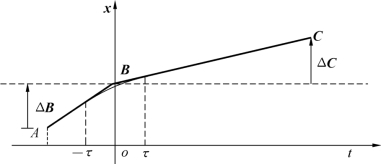
图6-8　两段轨迹间的过渡

在此时间区间[-τ，τ]，每一分量的加速度保持不变，其值为

式中：

矢量ΔC和ΔB的各元素分别为节点B到C和节点B到A的直角坐标距离和角度；T为机械手手部从节点B到C所需时间。

由式（6-38）可以得出相应的在区间-τ＜t＜τ中的速度和位移：

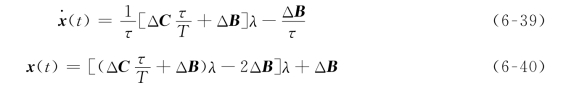
式中：

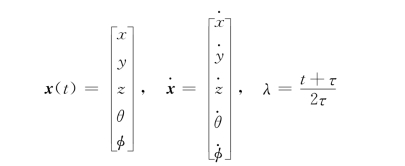
在时间区间τ＜t＜T内，运动方程为

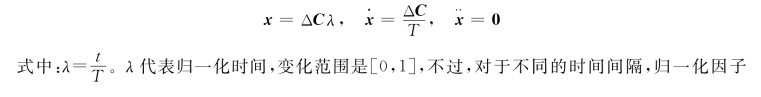
对于由A到B，再到C的运动，把ψ定义为在时间区间-τ＜t＜τ中运动的线性插值，即

式中的ψBC和ψAB分别是由A到B和由B到C的运动规定的，与式（6-35）类似。因此ψ将由ψAB变化到ψBC。

总之，为了从节点pi运动到pi+1，首先要由式（6-29）至式（6-37）算出驱动函数，然后按式（6-27）计算0T6（λ），再由运动学反解程序算出相应的关节变量。必要时，可在反解求出的节点之间再用二次多项式进行插值。

笛卡儿空间的规划方法不仅概念上直观，而且规划的路径准确。笛卡儿空间的直线运动路径规划仅仅是轨迹规划的一类，更加一般地，应包含其他轨迹，如椭圆、抛物线、正弦曲线等。可是，由于缺乏适当的传感器测量手部笛卡儿坐标，进行位置和速度反馈，因此笛卡儿空间路径规划的结果需要实时变换为相应的关节坐标，计算量很大，致使控制间隔较长。如果在规划时考虑机械手的动力学特性，就要以笛卡儿坐标给定路径约束，同时以关节坐标给定物理约束（例如，各电动机的容许力和力矩、速度和加速度极限），使得优化问题具有在两个不同坐标系中的混合约束。因此，笛卡儿空间规划存在由于运动学反解带来的问题。