关节速度传递机制

根据前述讨论有

d X（d X=[d x　d y　d z　dφxdφydφz]T）反映了操作空间的微小运动，它由机器人末端微小线位移（d x，d y，d z）和微小转动（dφxdφydφz）组成。

式（4-27）可变化为

即

式中：V——机器人末端在操作空间中的广义速度；

——机器人关节在关节空间中的关节速度；

J（q）——确定关节空间速度与操作空间速度V之间关系的雅可比矩阵。

因此，例4.2中二自由度机器人手部速度为

(www.xing528.com)

反之，假如给定机器人手部速度，则可由式（4-29）解出相应的关节速度，即

式中：J-1——机器人逆速度雅可比矩阵。

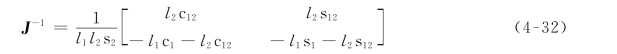
【例4.3】　某二自由度平面关节型机器人（见图4-2），其手部沿固定坐标系的x0轴正向以1 m/s的速度移动，杆长l1=l2=0.5 m。设在某瞬时θ1=30°，θ2=-60°，求相应瞬时的关节速度。

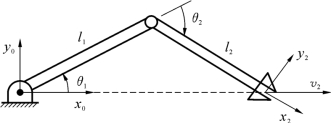
图4-2　二自由度平面关节型机器人的速度传递

解　由式（4-26）可知，二自由度机械手速度雅可比矩阵为

则其逆速度雅可比矩阵为

这里，分析一下例4.3的一种特殊情况。式（4-32）中，当l1l2s2=0时，J-1无解。当l1≠0，l2≠0，即θ2=0或θ2=180°时，二自由度机器人逆速度雅可比矩阵J-1奇异。这时，该机器人的两臂完全伸直或完全折回，机器人处于奇异形位。在这种奇异形位下，手部正好处在工作空间的边界上，手部只能沿着一个方向（即与臂垂直的方向）运动，不能沿其他方向运动，退化了一个自由度。