雅可比矩阵：定义及应用

上面分析了机器人的微分运动，基于此，我们研究机器人操作空间速度与关节空间速度间的线性映射关系，即雅可比矩阵。

机器人的操作速度与关节速度的线性变换定义为机器人的雅可比矩阵。

机械手的运动方程为

该方程表示了操作空间X与关节空间q之间的位移关系。机器人末端在操作空间的位置和方位可用末端手爪的位姿X表示，它是一个6维列矢量X=[x　y　z　φxφyφz]T。对于n自由度机器人的情况，关节变量可用广义关节变量q表示，q=[q1q2…　qn]T。

将式（4-17）两边对时间t求导：

J（q）——6×n的偏导数矩阵，称为机械手的雅可比矩阵，它的第i行第j列元素为

由式（4-20）有

把式（4-18）代入式（4-21）可得

即

含有n个关节的机器人，其雅可比矩阵J（q）是6×n的矩阵，前3行代表对机器人末端操作器线速度v的传递比，后3行代表对夹手的角速度ω的传递比，而每一列代表相应的关节速度q˙对机器人末端操作器线速度和角速度的传递比。这样，可把雅可比矩阵J（q）分块为

式中：Jli和Jai——关节i的单位关节运动引起的夹手的线速度和角速度。(www.xing528.com)

因此，可把夹手的线速度v和角速度ω表示为各关节速度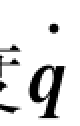的线性函数：

【例4.2】　二自由度平面关节型机器人（2R机器人）如图4-1所示，求其雅可比矩阵。

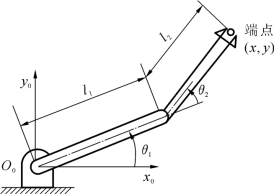
图4-1　二自由度平面关节型机器人

解　根据第3章建立运动学方程方法或者几何法，很容易求出手部端点位置（x，y）与旋转关节变量θ1，θ2的关系为

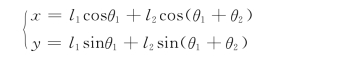
即

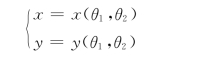
将其微分，得

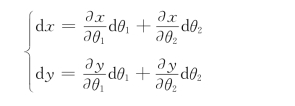
写成矩阵形式为

令d X=J dθ，可得

则J为2R机器人速度雅可比矩阵，它反映了关节空间微小运动dθ与手部工作空间微小位移d X之间的关系。

式中：s1=sinθ1；c1=cosθ1；s12=sin（θ1+θ2）；c12=cos（θ1+θ2）。