典型逆运动学案例分析

【例3.7】　求例3.6中的PUMA560机器人的运动学逆解。

解　根据式（3-31），运动学方程可以写成

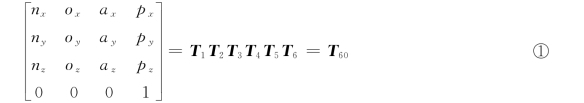
在逆运动学求解问题中，对于矩阵方程①，等式左边的矩阵元素是已知的，而等式右边的六个矩阵是未知的，需要求解θ1、θ2、θ3、θ4、θ5、θ6。

（1）求解θ1。

用逆变换左乘方程①，得

计算两边矩阵，令两端的元素（2，4）分别对应相等，可得

利用三角代换：

可得

式中：正负号对应于θ1的两个可能解。

（2）求解θ3。

令矩阵方程②两端的元素（1，4）和（3，4）分别对应相等，即得两方程：

式⑤与式⑥的平方和为

其中，

方程⑦中已经消去θ2，且方程⑦可采用三角代换求解θ3：

（3）求解θ2。

令方程⑨两边的元素（1，4）和（2，4）分别对应相等，可得(www.xing528.com)

可求得

由方程组⑩两式分母相等且为正，可进一步得

根据θ1、θ3解的四种可能组合，可以得到相应的四种可能值θ2+θ3，于是得到θ2的四种可能解：

（4）求解θ4。

因为式⑨的左边均已知，令两边元素（1，3）和（3，3）分别对应相等，则可得

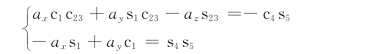
只要s5≠0，即可求出θ4为

当s5=0时，机器人处于奇异形位。此时，关节轴4和6同轴，只能解出θ4与θ6的和或差。

（5）求解θ5。

根据求出的θ4，即可求出θ5，将式①两端左乘逆变换有

由此可得到θ5的封闭解：

（6）求解θ6。

从而可求出θ6的封闭解：

通过以上计算，θ1有两个解、θ3有两个解，两两组合，是四种情况，对应θ2有四组解；每个θ2对应的θ4有两个解，所以对应的解共8组，如图3-19所示。

图3-19　PUMA560机器人的8组运动学逆解示意图

虽然根据以上分析，PUMA560机器人到达一个确定的目标位姿共有8组不同的解，但由于结构的限制，例如各关节变量不能都在360°范围内运动，因此有些解不能实现。在机器人有多个逆解时，应选取最合适的一组解，以满足机器人的工作要求。