逆运动学求解问题的优化方案

1.解的存在性

目标位置如果处于工作空间之外，则机器人逆运动学问题可能无解，如图3-15所示。如果目标位置处于工作空间内，那么至少存在一组解。需要注意的是，工作空间是一个三维空间，与每段连杆长度、每个关节旋转角的旋转范围等均有关系。

2.解的多重性

求解机器人逆运动学问题时，可能存在多个解。如图3-16所示，对于一个带有末端执行器的三连杆平面机器人，存在两组解。

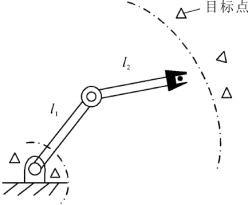
图3-15　目标点在工作空间外

图3-16　同一个目标点对应多个解

当逆运动学问题存在多组解时，一般可以采用如下方法排除多余解。

（1）根据关节运动空间来选择合适的解。

如求得机器人某关节角的两个解为

若当前该机器人关节角度为110°，则移动到40°所需时间较少，因此可选择θi1=40°。

（2）根据避障要求（或者其他约束条件），选择合适的解。

最短行程发生干涉，只能选择更长行程，如图3-17所示。

图3-17　较短行程存在障碍物

3.求解方法

一般把逆运动学的求解方法分为封闭解法和数值解法。这里为了便于理解，本章讲解封闭解法。封闭解法指的是解析形式的解法，具体包括代数解法和几何解法。

1）代数解法

运用变换矩阵的逆左乘，然后找出右端为常数的元素，并令这些元素与左端元素相等，这样就能得出一个可以求解的三角函数方程。重复上述过程，直到解出所有未知数，所以这种方法也叫分离变量法。下面以3.2.3节中例3.4的平面三连杆机器人（见图3-10，建立的坐标系见图3-11）为例介绍代数解法。

根据例3.4，求出平面三连杆机器人的正向运动学方程为

令式（3-32）和式（3-33）对应元素相等，可得到四个非线性方程：

根据式（3-34）至式（3-37）这四个方程，可求出θ1，θ2和θ3。

将式（3-36）与式（3-37）同时平方后对应相加，可得

可进一步求得

若式（3-38）右边的值不在范围[-1，1]内，则该目标点不在机器人工作空间内，逆运动学无解。假定目标点在工作空间内，则

根据式（3-38）和式（3-39），应用双变量反正切函数计算，可得θ2：

式（3-40）有正、负两组解，对应了该例中逆运动学的两组不同的解。(www.xing528.com)

根据上面求得的θ2、式（3-36）和式（3-37），可求出θ1。

假定

则式（3-36）和式（3-37）可写成

为求解这种形式的方程，可进行如下变量代换，令

则式（3-42）可写成

利用双变量反正切函数，可得

从而有

需要注意的是，θ2取值为正或负，决定了k2的正、负，因此而影响θ1的取值。若x=y=0，则式（3-47）的值不确定，θ1可取任何值。

最后，根据式（3-34）和式（3-35）能求出θ1，θ2和θ3的和φ：

从而可求出：

至此，完成了平面三连杆机器人的逆运动学求解。

2）几何解法

对于自由度较少的机器人，或者连杆扭角较特殊时（为0°或者90°），用几何解法求解运动学逆解是比较容易的。下面以平面两连杆为例来说明。

如图3-18所示，机器人末端处于P（x，y）点，OA、PA，以及连线OP组成了一个三角形。图3-18中关于连线OP，与OA、PA位置对称的一组点画线表示两连杆机器人的另一种可能的位形，该组位形同样可以达到点P的位置。

图3-18　几何法求解平面两连杆机器人运动学逆解

对于图3-18中实线表示的三角形（下部的机器人位形），根据余弦定理可以得到

求得连杆L1和L2之间的夹角α后，我们即可通过平面几何关系求出θ1和θ2：

如图3-18所示，当α′=π-α时，机器人有另外一组对称的解：

现在回到图3-11中的平面三连杆机器人，此处得到的两个解θ1，θ2也是图3-11中的前两段连杆的旋转角，而平面内的角度是可以直接相加的，因此三根连杆的角度之和即为最后一根连杆的方位角φ：

则可以解出θ3：

至此我们即用几何解法得到了这个机器人逆运动学的全部解。