典型案例：机器人正运动学方程

【例3.6】　PUMA560机器人是串联多关节型机器人，6个关节都是转动关节，具有6个自由度。前3个关节用于确定手腕中心参考点在空间的位置，后3个关节用于确定手腕姿态，其结构如图3-13所示。

图3-13　PUMA560结构示意图

（1）建立D-H坐标系。

建立的连杆坐标系如图3-14所示。

坐标系｛O0｝建在基座上。O0x0代表机器人的横方向，即肩关节轴线方向；O0y0代表机器人手臂的正前方；O0z0代表机器人身高方向。

关节1的轴线垂直；关节2、3的轴线水平，且平行；关节3和4的轴线垂直相交，距离为a3（可以忽略）。z轴建在各关节轴线上。

x1轴在水平面内，x2轴沿大臂轴线方向，x3轴与小臂轴线垂直，x4轴∥x5轴∥x6轴。

坐标原点之间的关系为：O0与O1相距h；O2与O3相距a3；O4与O5重合。

坐标系｛O6｝为终端坐标系，考虑了工具长度d6。

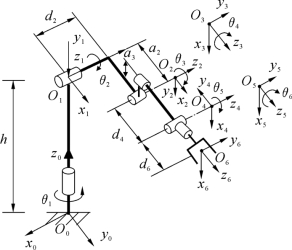
图3-14　连杆坐标系示意图

（2）确定各连杆的D-H参数（忽略h和a3）。

表3-4给出了各连杆的D-H参数。

表3-4　PUMA 560机器人连杆的D-H参数

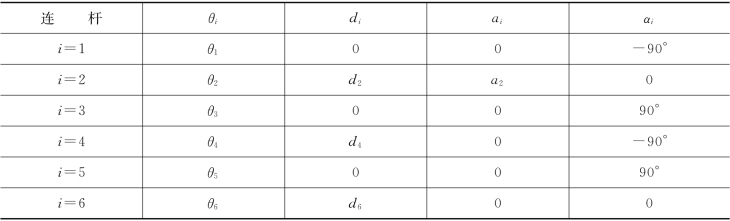
（3）求两杆之间的位姿矩阵Ti。

由表3-4和式（3-31）可求得Ti：(www.xing528.com)

式中：si=sinθi；ci=cosθi。

（4）求机器人的运动学方程。

式中：nx=c1[c23（c4c5c6-s4s6）-s23s5c6]-s1（s4c5c6+c4s6）；

ny=s1[c23（c4c5c6-s4s6）-s23s5c6]+c1（s4c5c6+c4s6）；

nz=-s23（c4c5c6-s4s6）-c23s5c6；

ox=c1[-c23（c4c5s6+s4c6）+s23s5c6]-s1（-s4c5c6+c4s6）；

oy=s1[-c23（c4c5s6+s4c6）+s23s5c6]+c1（-s4c5c6+c4s6）；

oz=s23（c4c5s6+s4c6）+c23s5c6；

ax=c1（c23c4s5+s23c5）-s1s4s5；

ay=s1（c23c4s5+s23c5）+c1s4s5；

ax=c1（c23c4s5+s23c5）-s1s4s5；

px=c1[d6（c23c4s5+s23c5）+s23d4+a2c2]-s1（d6s4s5+d2）；

py=s1[d6（c23c4s5+s23c5）+s23d4+a2c2]+c1（d6s4s5+d2）；

pz=d6（c23c5-s23c4s5）+c23d4-a2s2；

其中：cij=cos（θi+θj）；sij=sin（θi+θj）。