齐次坐标变换简介

1.齐次坐标的定义

空间中任一点在直角坐标系中的坐标用四维坐标表示，则该四维坐标即为直角坐标的齐次坐标。若有四个不同时为零的数与该点三个直角坐标分量之间存在以下关系：

则称（x′，y′，z′，k）是空间该点的齐次坐标。

关于齐次坐标的几点说明：

（1）空间中的任一点都可用齐次坐标表示；

（2）空间中的任一点的直角坐标是单值的，但其对应的齐次坐标是多值的；

（3）k是比例坐标，它表示直角坐标值与对应的齐次坐标值之间的比例关系；

（4）若比例坐标k=1，则空间任一点（x，y，z）的齐次坐标为（x，y，z，1），以后用到齐次坐标时，一律默认k=1。

2.齐次坐标变换矩阵

若坐标系｛Oj｝是｛Oi｝先沿矢量pij（pij=pxi+pyj+pzk，i，j，k是坐标系｛Oi｝对应坐标轴上的单位矢量）平移，再绕z轴旋转θ角得到的，则空间任一点在坐标系｛Oi｝和坐标系｛Oj｝中的矢量和对应的变换矩阵之间就有

写成矩阵形式则为

也即

进一步变换为

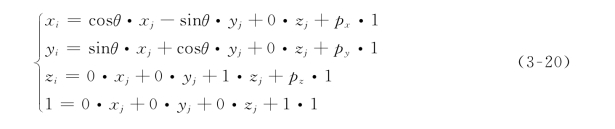
再将其写成矩阵形式，则有

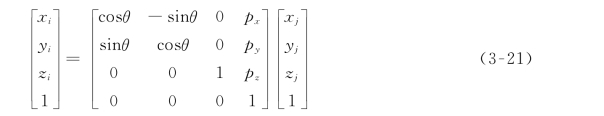
由此可得联合变换的齐次坐标方程为

齐次变换矩阵Mij为

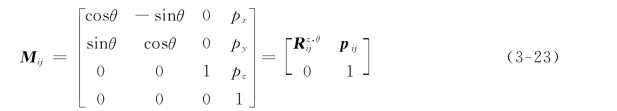
一般齐次变换矩阵Mij的通式可以表示为

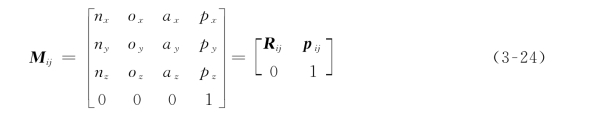
齐次变换矩阵的符号及齐次矩阵为

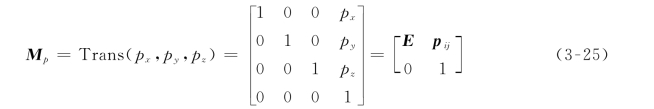
旋转变换的齐次矩阵为

当空间有n个坐标系时，若已知相邻坐标系之间的齐次变换矩阵，则

由此可知，建立机器人的坐标系，将机器人手部在空间的位姿用齐次坐标变换矩阵描述出来，可得到机器人的运动学方程。

【例3.2】　假设坐标系｛n，o，a｝位于参考坐标系｛x，y，z｝的原点，坐标系｛n，o，a｝上的点P（7，3，2）依次经历如下变换，求出变换后该点相对于参考坐标系的坐标。(www.xing528.com)

（1）绕z轴旋转90°；

（2）绕y轴旋转90°；

（3）平移[4，-3，7]。

解　绕z轴旋转90°对应的矩阵如下：

绕y轴旋转90°对应的矩阵如下：

平移[4，-3，7]，矩阵如下：

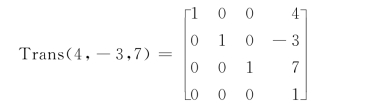
则变换后，坐标系｛n，o，a｝上的点P（7，3，2）在参考坐标系｛x，y，z｝中的坐标可按如下方法求出：

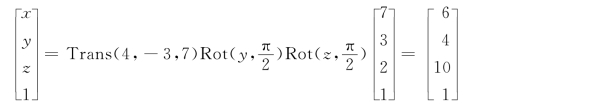
3.相对变换

坐标系之间多步齐次变换矩阵等于每次单独变换的齐次变换矩阵的乘积，而相对变换则决定这些矩阵相乘的顺序，即左乘和右乘：

（1）若坐标系之间的变换是始终相对于原来的参考坐标系，则齐次坐标变换矩阵左乘；

（2）若坐标系之间的变换是相对于当前新的坐标系，则齐次坐标变换矩阵右乘。

【例3.3】　设活动坐标系｛O′：u，v，w｝与固定坐标系｛O：x，y，z｝初始位置重合，依次经下列坐标变换：①绕z轴旋转90°；②绕y轴旋转90°；③相对于固定坐标系平移位置矢量4i-3j+7k。试求合成齐次坐标变换矩阵T。

解　活动坐标系绕固定坐标系z轴旋转90°，其齐次变换为

活动坐标系再绕固定坐标系y轴旋转90°，其齐次变换为

活动坐标系再平移4i-3j+7k，有

故合成齐次变换矩阵为

例3.3坐标变换的几何表示如图3-6所示。

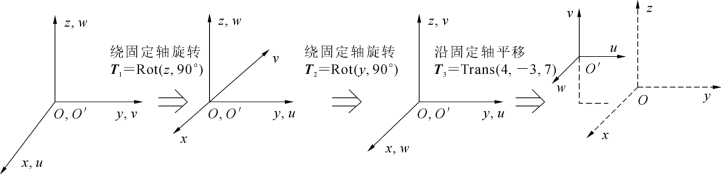
图3-6　坐标变换的几何表示

以上变换是相对固定坐标系进行的，这里尤其需要注意的是变换次序不能随意调换，因为矩阵的乘法不满足交换律，很容易举出这样的例子：Trans（4，-3，7）Rot（y，90°）≠Rot（y，90°）Trans（4，-3，7）；Rot（y，90°）Rot（z，90°）≠Rot（z，90°）Rot（y，90°）；等等。

上面所述的坐标变换每步都是相对于固定坐标系进行的，也可以相对于活动坐标系进行变换：坐标系｛O′：u，v，w｝初始与固定坐标系｛O：x，y，z｝相重合，首先相对于固定坐标系平移4i-3j+7k；然后绕活动坐标系的v轴旋转90°；最后绕w轴旋转90°。这时合成变换矩阵为

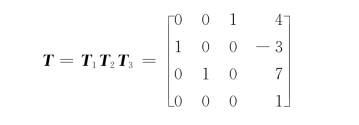
变换的几何表示如图3-7所示。

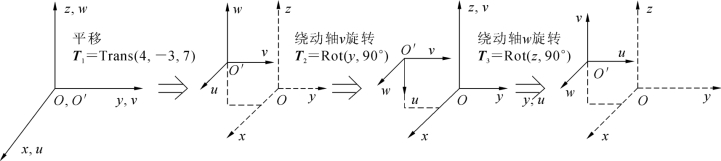
图3-7　绕活动坐标系变换的几何表示

经过以上分析，可以得到如下结论：若每次的变换是相对于固定坐标系进行的，则矩阵左乘；若每次的变换是相对于活动坐标系进行的，则矩阵右乘。