多项式回归优化技巧

1.多项式回归(Polynom ial Regression)算法原理

一般线性回归中，使用的假设函数是一元一次方程，也就是二维平面上的一条直线。但是很多时候可能会遇到直线方程无法很好地拟合数据的情况，这时可以尝试使用多项式回归。多项式回归中，加入了特征的更高次方(如平方项或立方项)，也相当于增加了模型的自由度，用来捕获数据中非线性的变化。

在多项式回归中，最重要的参数是最高次方的次数。设最高次方的次数为n，且只有一个特征时，其多项式回归的方程如式(4－18)所示。

如果令x0＝1，在多样本的情况下，可以写成向量化的形式:

式中，X是大小为m×(n＋1)的矩阵，θ是大小为(n＋1)×1的矩阵。在这里虽然只有一个特征x以及x的不同次方，但是也可以将x的高次方当作一个新特征。与多元回归分析唯一不同的是，这些特征之间是高度相关的，而不是通常要求的那样是相互对立的。

2.多项式回归(Polynom ial Regression)算法案例

扩展库sklearn.preprocessing中的PolynomialRegression类实现了多项式回归算法，其构造方法的语法格式如下:

def__init__(self,degree=2,*,interaction_only=False,include_bias=True,order='C')

常用参数如表4－16所示，常用方法如表4－17所示。

表4－16　Polynom ialRegression类常用参数

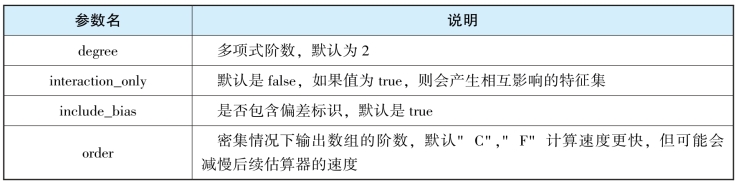
表4－17　LogisticRegression类常用方法

下面是用代码演示sklearn.preprocessing中的PolynomialRegression回归算法的原理。例4＿10分别将线性回归和多项式回归拟合到数据集，并用散点图呈现效果。

例4＿10＿PolynomialRegression.py

(www.xing528.com)

运行结果如图4－17所示。

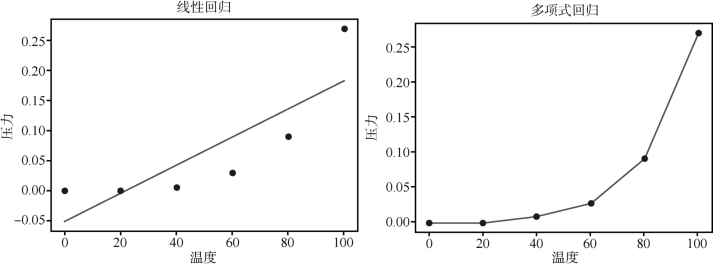
图4－17　LinearRegression与PolynomialRegression回归算法

课程思政小课堂

使用Python做数据分析的优点是什么?

最近几年，大数据的发展程度越来越明显，很多企业由于使用了大数据分析，朝着更好的方向发展，这就导致数据分析行业的人才开始稀缺起来，对于数据分析这个工作，是需要学会一些编程语言的，如MATLAB、Python、Java等语言。对于初学者来说，Python是一个不错的语言，Python语言简单易懂，同时对于大数据分析有很明显的帮助。

Python在数据分析和交互、探索性计算以及数据可视化等方面都显得比较活跃，这就是使用Python进行数据分析的原因之一。Python拥有numpy、matplotlib、scikitlearn、pandas、ipython等工具，在科学计算方面十分有优势，尤其是pandas，在处理中型数据方面可以说有着无与伦比的优势，已经成为数据分析工具中的中流砥柱。

Python也具有强大的编程能力，这种编程语言不同于R或者MATLAB，Python有一些非常强大的数据分析能力，并且还可以利用Python进行爬虫、写游戏以及自动化运维，Python在这些领域中有着很广泛的应用，这些优点使得一种技术可以解决所有的业务服务问题，充分体现了Python有利于各个业务之间的融合。使用Python能够大大提高数据分析的效率。

Python对于如今火热的人工智能也有一定的帮助，这是因为人工智能需要的是即时性，而Python是一种非常简洁的语言，同时有着丰富的数据库以及活跃的社区，这样就能够轻松提取数据，从而为人工智能提供优质的服务。

Python语言得益于它的简单方便，使得其在大数据、数据分析以及人工智能方面都有十分明显的存在感。对于数据分析从业者以及想要进入数据分析行业的人来说，简单易学、容易上手是一个很大优势，所以，要做好数据分析，一定要学会Python语言。

思考与练习

1.葡萄酒数据集(wine.data)搜集了法国不同产区葡萄酒的化学指标。建立决策树和SVM两种分类器模型，比较两种分类器在此数据集上的分类性能。

提示:每种分类器需要对参数进行尝试，找出此种分类算法的较优模型，再与其他分类器性能进行比较。

2.Iris(鸢尾花)数据集记录了山鸢尾、变色鸢尾和弗吉尼亚鸢尾三个不同种类鸢尾花的特征数据，包括4个特征项:花萼长度与宽度以及花瓣的长度与宽度，一个分类标签是花的类别。数据集共有150条记录。鸢尾花数据集是统计学家R.A.Fisher在20世纪中期发布的，被公认为数据挖掘最著名的数据集。

(1)使用K－means算法对鸢尾花数据集进行聚类分析。

(2)在互联网上收集任一事物的特征数据，构成数据集，保存在相应文件中，利用K－means算法对收集的数据集进行聚类分析。