逻辑回归原理与应用

1.逻辑回归(Logistic Regression)算法原理

线性回归模型的先决条件是所有的变量都是连续变量，随着自变量x的增加，因变量y也会增加。假设需要预测普通的中产阶级是否买得起房的问题，在这种情况下因变量是离散的，因变量只有买得起和买不起两个值。那么采用Logistic回归就可以用来基于自变量预测因变量的可能性，所以逻辑回归本身并不是回归算法而是分类算法。

逻辑回归基于逻辑函数f(x)，如式(4－14)所示。

当y→∞时，f(y)→1，当y→－∞时，f(y)→0，逻辑函数f(y)的值随着y值增大而增大，且在0～1之间变化。

因为逻辑函数f(y)的取值范围是(0，1)，所以可以用来作为某一特定结果的概率值，随着y值的增加，f(y)值代表的概率也会增加。在逻辑回归中，我们令y表示因变量的一个线性函数:

而基于自变量x1，x2，…，xn，事件发生的概率p为

线性回归中y代表因变量，而在逻辑回归中f(y)代表因变量(通常只取0或1)，y只是作为一个中间结果，不能被直接观察到。若用p表示f(y)，则公式可重写为

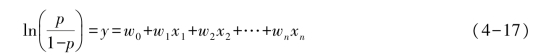
通过这种方式将其由非线性转换为线性，然后计算出最优的w0，w1，…，wn，得到逻辑回归模型。

2.逻辑回归(Logistic Regression)算法案例

扩展库sklearn.linear＿model中的LogisticRegression类实现了逻辑回归算法，其构造方法的语法格式如下:(www.xing528.com)

def__init__(self,penalty='l2',dual=False,tol=0.0001,C=1.0,fit_intercept=True,intercept_scaling=1,class_weight=None,random_state=None,solver='warn',max_iter=100,multi_class='warn',verbose=0,warm_start=False,n_jobs=None)

常用参数如表4－14所示，常用方法如表4－15所示。

表4－14　LogisticRegression类常用参数

表4－15　LogisticRegression类常用方法

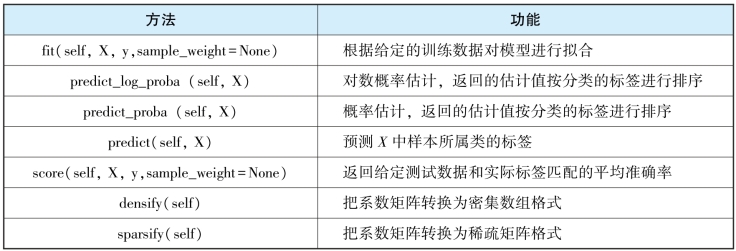
下面是用代码演示sklearn.linear＿model中的LogisticRegression回归算法的原理。例4＿9运用数据集创建并训练逻辑回归模型进行数据测试。

例4＿9＿LogisticRegression.py

运行结果如图4－16所示。

图4－16　LogisticRegression回归算法