线性回归是一种用来对若干输入变量与一个连续的结果变量之间关系建模的分析技术，其假设输入变量与结果变量之间的关系是一种线性关系。线性回归模型的任务是通过基于变量的数值，解释并预测因变量。如果只考虑一个自变量的情况，则线性回归的目标就是寻找一条直线，使得给定一个自变量值可以计算出因变量的值。
线性回归问题中预测目标是实数域上的数值，优化目标简单，是最小化预测结果与真实值之间的差异。样本数量为m的样本集，特征向量X＝{x1，x2，…，xm}，对应的回归目标y＝{y1，y2，…，ym}。线性回归则是用线性模型刻画特征向量X与回归目标y之间的关系:
使得f(xi)≅yi，关于w和b的确定，其目标是使f(xi)和yi的差别尽可能小。如何衡量两者之间的差别呢?在回归任务中常用的标准为均方误差。基于均方误差最小化的模型求解方法称为最小二乘法，即找到一条直线使样本到直线的欧式距离最小。基于此思想，损失函数L可以被定义为
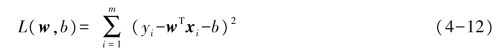
求解w、b使得损失函数最小化的过程，称为线性回归模型的最小二乘“参数估计”。
以上则为最简单形式的线性模型，但是可以有一些变化，可以加入一个可微函数g，使得y和f(x)之间存在非线性关系，形式如下:
这样的模型被称为广义线性模型，函数g被称为联系函数。
2.线性回归(Linear Regression)算法案例(www.xing528.com)
使用扩展库sklearn.linear＿model模块中拥有可以直接使用的线性回归模型(LinearRegression)，只需要将数据集导入，然后放入模型进行训练。采用Sklearn进行多元回归模型的构建只需以下步骤:
(1)获取数据集:Sklearn库的datasets包含Boston数据集，直接导入即可。
(2)构建多元回归模型:导入LinearRegression，采用cross＿cal＿predict进行十折交叉验证并返回预测结果。
(3)预测结果与结果可视化:采用matplotlib绘制预测值与真实值的散点图，并使用matplotlib.pyplot.show()演示。
例4＿8＿LinearRegression.py
二维码4－4 线性回归
运行结果如图4－15所示。
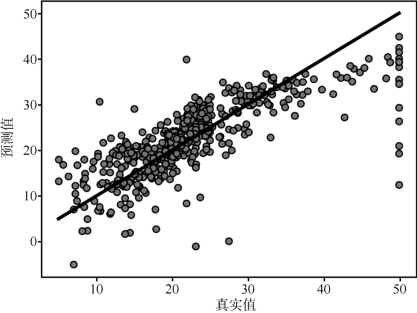
图4－15 LinearRegression运行结果
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
