数据科学技术：FP-Tree算法详解

FP－Tree算法同样用于挖掘频繁项集。其中引入了三部分内容来存储临时数据结构。首先是项头表，记录所有频繁1－项集(支持度大于最小支持度的1－项集)的出现次数，并按照次数进行降序排列。其次是FP树，将原始数据映射到内存，以树的形式存储。最后是节点链表，所有项头表里的频繁1－项集都是一个节点链表的头，它依次指向FP树中该频繁1－项集出现的位置，将FP树中所有出现相同项的节点串联起来。

FP－Tree算法首先需要建立降序排列的项头表，然后根据项头表中节点的排列顺序对原始数据集中每条数据的节点进行排序并剔除非频繁项，得到排序后的数据集。具体过程如图4－7所示。

图4－7　项头表及排序后的数据集

建立项头表并得到排序后的数据集后，建立FP树。FP树的每个节点由项和次数两部分组成。逐条扫描数据集，将其插入FP树，插入规则为:每条数据中排名靠后的作为前一个节点的子节点，如果有公用的祖先，则对应的公用祖先节点计数加1。插入后，如果有新节点出现，则项头表对应的节点会通过节点链表链接上新节点。所有的数据都插入FP树后，FP树的建立完成。图4－8展示了向FP树中插入第二条数据的过程，图4－9所示为构建好的FP树。

图4－8　向FP树中插入第二条数据的过程

图4－9　FP树(www.xing528.com)

得到FP树后，可以挖掘所有的频繁项集。从项头表底部开始，找到以该节点为叶子节点的子树，可以得到其条件模式基。基于条件模式基，可以递归发现所有包含该节点的频繁项集。以D节点为例，挖掘过程如图4－10所示。D节点有两个叶子节点，因此首先得到的FP子树如图4－10左侧所示，接着将所有的祖先节点计数设置为叶子节点的计数，即变成{A:2，C:2，E:1，G:1，D:1，D:1}。此时E节点和G节点由于在条件模式基里面的支持度低于阈值而被删除了。最终在去除低支持度节点并不包括叶子节点后，D节点的条件模式基为{A:2，C:2}，如图4－10所示。通过它，我们很容易得到D节点的频繁2－项集为{A:2，D:2}和{C:2，D:2}。递归合并频繁2－项集，得到频繁3－项集为{A:2，C:2，D:2}。D节点对应的最大频繁项集为频繁3－项集。

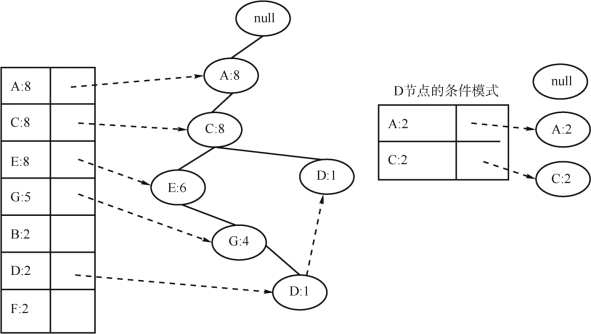
图4－10　频繁项集挖掘过程

算法具体流程如下:

(1)首先扫描数据，得到所有频繁1－项集的计数。然后删除支持度低于阈值的项，将频繁1－项集放入项头表，并按照支持度降序排列。

(2)扫描数据，将读到的原始数据剔除非频繁1－项集，并按照支持度降序排列。

(3)读入排序后的数据集，插入FP树。按照排序后的顺序进行插入，排序靠前的节点是祖先节点，而靠后的节点是子孙节点。如果有公用的祖先，则对应的公用祖先节点计数加1。插入后，如果有新节点出现，则项头表对应的节点会通过节点链表链接上新节点。所有的数据都插入FP树后，FP树的建立完成。

(4)从项头表的底部项依次向上找创项头表项对应的条件模式基、从条件模式基递归挖掘得到项头表项的频繁项集。

(5)如果不限制频繁项集的项数，则返回步骤(4)所有的频繁项集，否则只返回满足项数要求的频繁项集。