支持向量机分类方法简介

1.支持向量机原理

在学习支持向量机算法之前，先看一个脑筋急转弯，在图4－2中画一条直线对多边形进行分隔来得到两个三角形，那么应该怎样画这条直线呢?

聪明的朋友应该已经想到了。在问题描述中要求画一条直线，但并没有限制直线的粗细，如果我们可以画一条很粗的直线，那么就有很多种分隔的方法，其中一种画法如图4－3所示。

图4－2　多边形

图4－3　画一条直线分隔多边形得到两个三角形

接下来再看图4－4，在二维平面上凌乱地摆放着两类物体，分别使用加号和减号表示，要求画一条直线把这两类物体分隔开。可知，这样的直线可以有多种画法，但是哪种更好呢?很明显，对于图中的两条直线，L2比L1要好很多，因为这样的直线和两类物体的距离最大，两个类别之间的间隔最大。如果有新物体加入，误分类的概率更小。毕竟分类器的目的不仅是划分已知的训练数据，更重要的是尽可能准确地划分未知数据。

在图4－4中，最接近于分隔直线L2的样本称作支持向量，直线L2两侧的阴影区域(或者说那条很粗的直线)的宽度称作间隔。

图4－4　分隔平面上随意摆放的两类物体

支持向量机(Support Vector Machine，SVM)是通过寻找超平面对样本进行分隔从而实现分类或预测的算法，分隔样本时的原则是使间隔最大化，寻找间隔最大的支持向量；在二维平面上相当于寻找一条“最粗的直线”把不同类别的物体分隔开，或者说寻找两条平行直线对物体进行分隔，并使得这两条平行直线之间的距离最大。如果样本在二维平面上不是线性可分的，无法使用一条简单的直线将其完美分隔开，可尝试通过某种变换把所有样本都投射到高维空间中，可以找到一个超平面将不同类的点分隔开。

SVM采用核函数(Kermel Function)将低维数据映射到高维空间，选用适当的核函数，就能得到高维空间的分割平面，较好地将数据集划分为两部分。研究人员提出了多种核函数，以适应不同特性的数据集。常用的核函数有线性核、多项式核、高斯核和sigmoid核等。核函数的选择是影响SVM分类性能的关键因素，若核函数选择不合适，则意味着将样本映射到不合适的高维空间，无法找到分割平面。当然，即使采用核函数，也不是所有数据集都可以被完全分割的，因此SVM的算法中添加了限制条件，来保证尽可能减少不可分点的影响，使划分达到相对最优。

2.支持向量机实现

案例:银行投资业务推广预测。

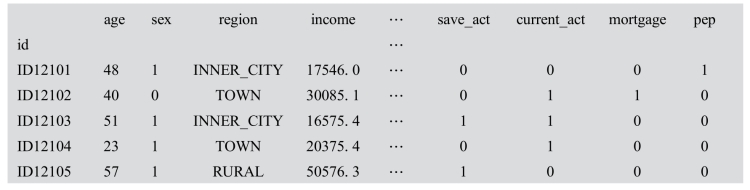
某银行客户数据集中包含客户的年龄、孩子个数、收入等11个特征项，其中“客户是否接受了银行邮件推荐的个人投资计划”(pep)是相应的分类标签(二分类)，前5条数据如图4－5所示。数据样本共有600个，没有缺失数据，保存在bankpep.csv文件中。

图4－5　银行业务推广客户数据集

scikit－learn的SupportVectorClassficat器的初始化函数如下。

clf＝svm.SVC(kernel＝，gamma，C，…)ion类实现SVM分类，只支持二分类，多分类问题需转化为多个二分类问题处理。SVM分类方法参数说明如表4－2所示。

表4－2　SVC分类方法参数说明

注:SVM分类实现其他函数与决策树一致，不再单独说明。

例4＿3＿SVM:使用scikit－learn建立SVM模型预测银行客户是否接受推荐的投资计划，并评估分类器的性能。

(1)从文件中读取数据，通常特征项“id”是由数据库系统生成的，不具有任何意义，读入时作为列索引读入。

(2)SVM算法只能使用数值型变量作为输入，需要将所有的特征值“YES”或“NO” 转换为1或0，“sex”特征值“FEMALE”和“MALE”也转换为1和0。(www.xing528.com)

由于有6个特征的值均为“YES”“NO”，将这些特征的标签放入一个序列，就可以通过for循环对特征逐个替换。

替换后，执行结果如下:

(3)特征项region、child的取值超过两个，且没有大小意义，应采用独热编码(onehoteocding)进行转化，如region有4种取值，那么region列转换为4列，其中取值对应的列为1，其余为0。然后将原DataFrame中的region和child列删除，再将生成的二元矩阵连接上去。

执行结果如下:

(4)在DataFrame数据对象，'pep'列存放分类标签，取出其值作为y，其余列的值为X。

执行结果如下:

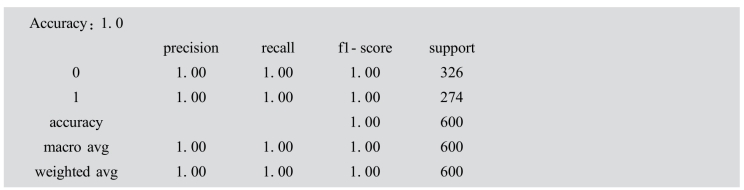
这里用所有的样本训练SVM分类器，预测准确率为100%。

(5)将数据集划分为测试集和训练集，在测试集上评估预测性能。

执行结果如下:

这时我们发现分类器在训练集上准确率能够达到100%，但在测试集上准确率只有50%～60%，效果极差。

(6)SVM算法需要计算样本点之间的距离，为了保证样本各个特征项对距离计算的贡献相同，需对数值型数据做标准化处理。标准化处理有很多计算方法，这里将每列标准化为标准正态分布数据。

执行结果如下:

先对整个数据集进行标准化，然后再切分为训练集和测试集，训练得到的分类器在测试集上的准确率提高到69%。

(7)通过调整模型初始化参数，进一步优化分类器模型。如kemel＝'poly'，gamma＝0.6，C＝0.001，分类器在测试集上的准确率进一步提高到80%。