朴素贝叶斯分类方法简介

1.基本概念

朴素贝叶斯算法是基于贝叶斯理论的概率算法，在学习其原理和应用前，先了解几个相关概念。

1)随机试验

随机试验是指可以在相同条件下重复试验多次，所有可能发生的结果都是已知的，但每次试验到底会发生其中哪一种结果是无法预先确定的。

2)事件与空间

在一个特定的试验中，每个可能出现的结果称作一个基本事件，全体基本事件组成的集合称作基本空间。

在一定条件下必然会发生的事件称作必然事件，可能发生也可能不发生的事件称作随机事件，不可能发生的事件称作不可能事件，不可能同时发生的两个事件称作互斥事件，二者必有其一发生的事件称作对立事件。

例如，在水平地面上投掷硬币的试验中，正面朝上是一个基本事件，反面朝上是一个基本事件，基本空间中只包含这两个随机事件，并且二者既为互斥事件又为对立事件。

3)概率

概率是用来描述在特定试验中一个事件发生可能性大小的指标，是介于0和1之间的实数，可以定义为某个事件发生的次数与试验总次数的比值，即

式中，nx表示事件x发生的次数，n表示试验总次数。

4)先验概率

先验概率是指根据以往的经验和分析得到的概率。

例如，投掷硬币实验中，50%就是先验概率。再如，有5张卡片，上面分别写着数字1、2、3、4、5，随机抽取一张，取到偶数卡片的概率是40%，这也是先验概率。

5)条件概率

条件概率也称作后验概率，是指在另一个事件B已经发生的情况下，事件A发生的概率，记为P(A｜B)。如果基本空间只有两个事件A和B，则有

或

以及

式中，A∩B表示事件A和B同时发生，当A和B为互斥事件时，有P(A∩B)＝0，容易得知，此时也有P(A｜B)＝P(B｜A)＝0。

仍以上面随机抽取卡片的试验为例，如果已知第一次抽到偶数卡片并且没有放回去，那么第二次抽取到偶数卡片的概率则为25%，这就是后验概率。

作为条件概率公式的应用，已知某校大学生英语四级考试通过率为98%，通过四级之后才可以报考六级，并且已知该校学生英语六级的整体通过率为68.6%，那么通过四级考试的那部分学生中有多少通过了六级呢?

在这里，使用A表示通过英语四级，B表示通过英语六级，那么A∩B表示既通过四级又通过六级，根据上面的公式有

可知，在通过英语四级考试的学生中，有70%的学生通过了英语六级。

6)全概率公式

已知若干互不相容的事件Bi，其中i＝1，2，…，n，并且所有事件Bi构成基本空间，那么对于任意事件A，有

这个公式称作全概率公式，可以把复杂事件A的概率计算转化为不同情况下发生的简单事件的概率求和问题。

例如，仍以上面描述的抽取卡片的试验为例，从5个卡片中随机抽取一张不放回，然后再抽取一张，第二次抽取到奇数卡片的概率是多少?(https://www.xing528.com)

使用A表示第一次抽取到偶数卡片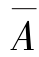，表示第一次抽取到奇数卡片，B表示第二次抽取奇数卡片。B事件发生的概率是由事件A和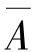这两种情况决定的，所以，根据全概率公式，有

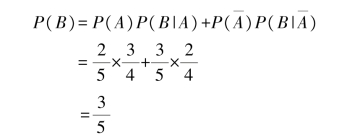
可知，第二次抽到奇数卡片的概率为60%。

7)贝叶斯理论

贝叶斯理论用来根据一个已发生事件的概率计算另一个事件发生的概率，即

或

2.朴素贝叶斯算法分类的原理与sklearn实现

朴素贝叶斯算法之所以说“朴素”，是指在整个过程中只做最原始、最简单的假设，例如，假设特征之间互相独立并且所有特征同等重要。

使用朴素贝叶斯算法进行分类时，分别计算未知样本属于每个已知类的概率，然后选择其中概率最大的类作为分类结果。根据贝叶斯理论，样本x属于某个类c的概率计算公式为

然后在所有条件概率P(c1｜x)，P(c2｜x)，…，P(cn｜x)中选择最大的那个，例如P(ck｜x)，并判定样本x属于类ck。

例如，如果邮件中包含“发票”“促销”“微信”或“电话”之类的词汇，并且占比较高或组合出现，那么这封邮件是垃圾邮件的概率会比没有这些词汇的邮件要大一些。

在扩展库sklearm.naive＿bayes中提供了三种朴素贝叶斯算法，分别是伯努利朴素贝叶斯BemoulliNB、高斯朴素贝叶斯GaussianNB和多项式朴素贝叶斯MultinomialNB，分别适用于伯努利分布(又称作二项分布或0－1分布)、高斯分布(也称作正态分布)和多项式分布的数据集。

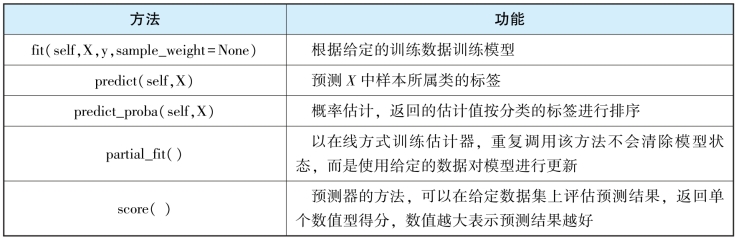
以高斯朴素贝叶斯GaussianNB为例，该类对象具有fit()、predict()、predict＿proba()、partial＿fit()、score()等常用方法，如表4－1所示。

表4－1　GaussianNB常用方法

案例:使用该算法对电子邮件进行分类。

(1)从电子邮箱中收集足够多的垃圾邮件和非垃圾邮件的内容作为训练集。

(2)读取全部训练集，删除其中的干扰字符，如【】*。、，等，然后分词，再删除长度为1的单个字，这样的单个字对于文本分类没有贡献，剩下的词汇认为是有效词汇。

(3)统计全部训练集中每个有效词汇出现的次数，截取出现次数最多的前N(可以根据实际情况进行调整)个。

(4)根据每个经过步骤(2)预处理后的垃圾邮件和非垃圾邮件内容生成特征向量，统计第(3)步中得到的N个词语分别在该邮件中出现的频率。每个邮件对应于一个特征向量，特征向量长度为N，每个分量的值表示对应的词语在本邮件中出现的次数。例如，特征向量[3，0，0，5]表示第一个词语在本邮件中出现了3次，第二个和第三个词语没有出现，第四个词语出现了5次。

(5)根据步骤(4)中得到特征向量和已知邮件分类创建并训练朴素贝叶斯模型。

(6)读取测试邮件，参考步骤(2)，对邮件文本进行预处理，提取特征向量。

(7)使用步骤(5)中训练好的模型，根据步骤(6)提取的特征向量对邮件进行分类。

下面的代码创建多项式朴素贝叶斯分类模型，使用151封邮件的文本内容(0.txt～150.txt)进行训练，其中0.txt～126.txt为垃圾邮件的文本内容，127.txt～150.txt为正常邮件的文本内容。模型训练结束后，使用5封邮件的文本内容(151.txt～155.txt)进行测试。

例4＿2＿Psbys.py

执行结果如下: