数值归约：簇采样与z分数规范化

数值归约(Numerosity Reduction)用替代的、较小的数据表示形式换原始数据。这些技术可以是参数或者非参数的。对于参数方法而言，使用模型估计数据，一般只需要存放模型参数而不是实际数据(离群点需存放)，如回归和对数－线性模型。

1.有参数方法

有参数方法是使用一个模型来评估数据，只需存放参数，而不需要存放实际数据，如回归模型和对数线性模型。

(1)回归模型:在简单的线性回归中，对数据建模，使之拟合到一条直线，用来近似给定数据。例如，可以用以下公式:

将随机变量y(称作因变量)表示为另一随机变量x(称为自变量)的线性函数，假设y的方差是常量。在数据挖掘中，y和x是数值数据库属性，回归系数w和b分别为直线的斜率和y轴截距。回归系数可用最小二乘法求解，即最小化数据的实际直线与该直线的估计之间的误差。

(2)对数线性模型:对数线性模型(Log－Linear Model)近似离散的多维概率分布。给定n维元组的集合，可把每个元组看作n维空间的点。对于离散属性集，可用对数线性模型，基于维族和的一个较小子集，估计多维空间中每个点的概率，这使得高维数据空间可以由较低维数据空间构造。对数线性模型也可用于维度归约和数据平滑。

2.非参数方法

存放数据归约表示的非参数方法包括:直方图、聚类、抽样和数据立方体聚类。

(1)直方图:直方图使用分箱来近似数据分布，是一种流行的数据归约形式。属性A的直方图(Histogram)将A的数据分布划分为不相交的子集或桶。如果每个桶只代表单个属性值/频率对，则该桶称为单值桶。桶表示给定属性的一个连续区间。等宽直方图中，每个桶的宽度区间是相等的。等频(等深)直方图中，每个桶大致包含相同个数的邻近数据样本。对于近似稀疏和稠密数据，以及高倾斜和均匀的数据，直方图是有效的。图3－10所示为一个直方图。

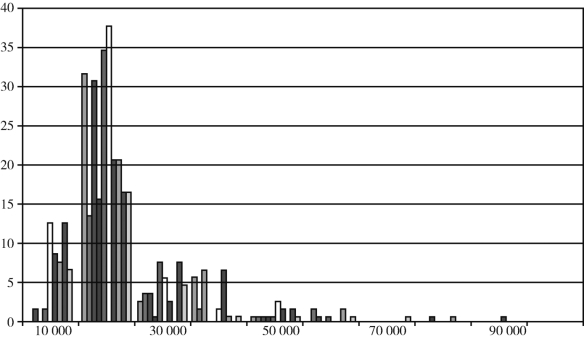
图3－10　直方图

(2)聚类:聚类技术把数据元组看作对象，将对象划分为群或簇，使得在一个簇中的对象相互相似，而与其他簇中的对象相异。通常，相似性基于距离函数，用对象在空间中的接近程度定义。簇的质量用直径表示，直径是簇中两个对象的最大距离。形心距离是簇质量的另一种度量，定义为簇中每个对象到簇形中(表示平均对象，或簇空间中的平均点)的平均距离。在数据归约中，用数据的簇代表替换实际数据，其有效性依赖数据的性质。对于被污染的数据，能够组织成不同簇的数据，比较有效。例如，图3－11是原始数据，图3－12是簇采样数据。

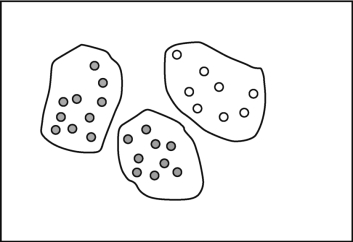
图3－11　原始数据

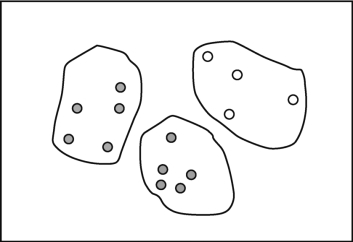
图3-12　簇采样数据

(3)抽样:抽样可以作为一种数据归约的技术使用，因为它允许用数据小得多的随机样本表示数据集，如图3－13所示。

①s个样本的无放回简单随机抽样(SRSWOR):从N个元组中抽取s个样本(s<N)，其中任意元组被抽取的概率均为1/N(等可能的)。

②s个样本的有放回简单随机抽样(SRSWR):一个元组被抽取后，又被放回数据集中，以便再次被抽取。

③簇抽样:数据集放入M个互不相交的簇，可以得到s个簇的简单随机抽样(SRS)，s<M。

④分层抽样:数据集被划分成互不相交的部分，称为“层”。数据是倾斜的时，可以帮助确保样本的代表性(如按季度或年龄分层)。

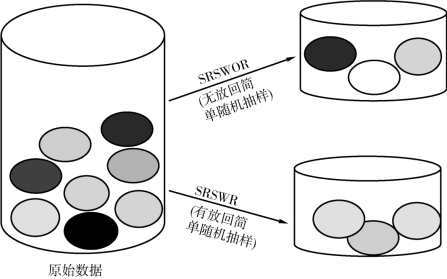
图3－13　数据抽样(www.xing528.com)

(4)数据立方体聚集:数据立方体存储多维聚集信息。每个属性都可能存在概念分层，允许在多个抽象层进行数据分析。数据立方体提供对预计算的汇总数据进行快速访问，适合联机数据分析和数据挖掘。在最低抽象层创建的立方体称为基本方体(Base Cuboid)。最高层抽象的立方体称为顶点方体(Apex Cuboid)。数据立方体聚集帮助我们从低粒度的数据分析聚合成汇总粒度的数据分析。我们认为表中最细的粒度是一个最小的立方体，在此之上每个高层次的抽象都能形成一个更大的立方体。例如，图3－14是某公司分店2008－2010年的销售数据。左部销售数据按照季度显示，右部数据聚集提供年销售额。

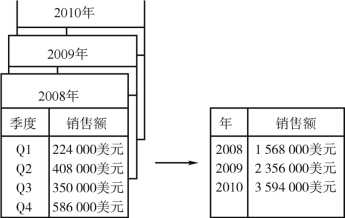
图3－14　销售数据

课程思政小课堂

pandas pipe:一种更优雅的数据预处理方法!

预处理是数据分析中必不可少的工程。预处理之所以重要，是因为它会对后续的数据分析质量、模型预测精度产生极大影响。在实际项目中拿到的数据往往是杂乱无章的(数据缺失、数据不一致、数据重复等)，要想得到理想结果，就必须通过一些恰当的分析方法提高数据质量，而这就是预处理的工作。在本书中，我们将重点讨论一个将「多个预处理操作」组织成「单个操作」的特定函数:pipe()。如例3＿6＿pandas pipe().py中的“(my＿df.pipe(fill＿missing＿values).pipe(drop＿duplicates，"id").pipe(remove＿outliers，["A"，"B"]))”操作，是集处理缺失值、去除重复值、删除异常值等多个预处理于一体的管理。

通过数据预处理，旨在培养学生的创新精神、自主创新意识和精益求精精神，培养学生成为21世纪的责任担当者、问题解决者和优雅生活者。

思考与练习

1.简述常见的噪声数据的处理方法。

2.列举属性值冲突问题的解决方法。

3.编程实现:基于本书中3.1.2小节实现学生调查反馈数据的去重操作。

4.如下规范化方法的值域是什么?

(1)最小－最大规范化。

(2)z分数规范化。

(3)z分数规范化，使用均值绝对偏差而不是标准差。

(4)小数定标规范化。

5.假设12个销售记录价格已经排序，如下所示:5、10、11、13、15、35、50、55、72、92、204、215。使用如下方法使它们划分成三个箱进行离散化。

(1)等频(等深)划分。

(2)等宽划分。

(3)聚类。

【注释】

[1]1英寸＝2.54厘米。

[2]1公斤＝1 000克。

[3]1磅＝0.453 6千克。