如何处理数据缺失问题

缺失值，指的是缺少的数据，这是最常见的数据问题。数据分析过程中会面对很多缺失值，其产生原因不同，有的是由于隐私的原因故意隐去，有的是变量本身就没有数值，有的是数据合并时不当操作产生的数据缺失。客观来看，缺失值产生的原因主要分为机械原因和人为原因。机械原因是由于机械原因导致的数据收集或保存的失败造成的数据缺失，如数据存储的失败、存储器损坏、机械故障导致某段时间数据未能收集(对于定时数据采集而言)。人为原因是由于人的主观失误、历史局限或有意隐瞒造成的数据缺失，如在市场调查中被访人拒绝透露相关问题的答案。

缺失值的处理方法主要分为三类:删除记录、数据插补和不处理。因此，从总体上来说分为删除存在缺失值的个案和对缺失值的插补。对于主观数据，人将影响数据的真实性，存在缺失值的样本，其他属性的真实值不能保证，那么依赖于这些属性值的插补也是不可靠的，所以对于主观数据一般不推荐插补的方法。插补主要是针对客观数据，可靠性有保证。

1.删除记录

删除记录，即删除含有缺失值的个案。删除记录主要有简单删除法和权重法。简单删除法是对缺失值进行处理的最原始方法，它将存在缺失值的个案删除。如果数据缺失问题可以通过简单地删除小部分样本来得到解决，那么可以采用简单删除法。当缺失值的类型为非完全随机缺失时，可以通过对完整的数据加权来减小偏差。把数据不完全个案标记后，将完整的数据个案赋予不同的权重，个案的权重可以通过logistic或probit回归求得。对于存在多个属性缺失的情况，需要对不同属性的缺失组合赋予不同的权重，这将大大增加计算的难度，降低预测的准确性，这时权重法并不理想。

2.数据插补

数据插补，也称可能值插补缺失值。其思想来源是:以最可能的值来插补缺失值比全部删除不完全样本所产生的信息丢失要少。常用的数据插补方法如表3－1所示，按照手段来说，可以分为以下三类:以业务知识或经验推测填充缺失值；以同一指标的计算结果(均值、中位数、众数等)填充缺失值；以不同指标的计算结果填充缺失值。常用的插值法有拉格朗日插值法、牛顿插值法、Hermite插值法、分段插值法、样条插值法等。

表3－1　常用的数据插补方法

例3＿1＿Lagrange Interpolation.py

pandas是Python中一个数据分析与清洗的库，是基于numpy库构建的。numpy是Python中科学计算的第三方库，代表“Numeric Python”。pandas作为在Python中一个数据分析与清洗的库，在数据清洗中主要用于处理数据缺失值、处理数据重复值和数据合并。

实验结果如图3－1所示。左侧为原始数据，右侧为插值后的处理效果。拉格朗日插值法在进行插值之前，会对数据进行异常值检测，发现数据大于7 000的，要对此日期对应的数据定义为空缺值，然后进行补数。利用拉格朗日插值对缺失的2015/2/14这天的原始销量数据进行插补，结果是4 156.86。对比分析，这天是周末，而周末的销售额一般要比周一到周五多，所以插值结果比较符合实际情况。从图3－1中可以看出，经拉格朗日插值法后的空缺值会得以补充，其他值均保持正常。

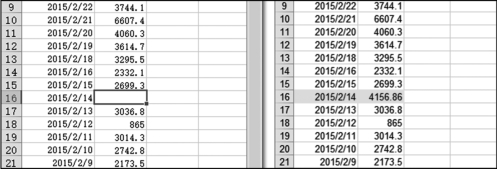
图3－1　拉格朗日插值法处理缺失值效果图

在实际操作中，缺失数据的处理方法主要有cleaned方法、dropna方法、isnull方法、fillna方法。如果想丢弃pandas中任何含有数据缺失值的行，可以使用cleaned方法来实现。如果想表明哪些数据是缺失值NaN，可以使用isnull方法来实现。

如果只想丢弃全为NaN的行，基于DataFrame的dropna()方法可用how＝'all'来实现，一般格式如下:

DataFrame.dropna(axis,how,thresh,…)

相关参数说明:axis值默认为0，表示为按行滤除，设为1时表示按列滤除。how＝'all' 表示丢弃全为NaN的行或列。thresh表示只保留有效数据数≥thresh值的行或列。DataFrame是一个表格型的数据类型。它含有一组有序的列，每列可以是不同的类型(数值、字符串等)。DataFrame类型既有行索引又有列索引，因此它可以看作是由Series组成的字典。Series和DataFrame是pandas库中两个最基本的数据类型。Series是能够保存任何类型的数据(整数、字符串、浮点数、Python对象等)的一维标记数组，并且每个数据都有自己的索引。此外，数据清洗时，为了方便展示数据，需用到matplotlib库。

例3＿2＿dropna().py(www.xing528.com)

运行结果如下:从缺失值的所属属性上讲，原有数据缺失值的属性不一，有的是成绩，有的是年龄，有的是体重，有的是月生活费，属于任意缺失。即如果所有的缺失值都是同一属性，那么这种缺失称为单值缺失；如果缺失值属于不同的属性，称为任意缺失。使用stu.dropna()对原有数据处理后，含有缺失项的原始数据序号为1、3、5的行被滤除；使用stu.dropna(thresh＝8)对原有数据处理后，有效数据个数为7的第五行数据被滤除，即只保留缺失1项或者信息不缺失的学生调查数据，缺2项及以上信息的被删除。

此外，从缺失的分布来看，缺失值可以分为完全随机缺失、随机缺失和完全非随机缺失。其中，完全随机缺失(Missing Completely at Random，MCAR)指的是数据的缺失是随机的，数据的缺失不依赖于任何不完全变量或完全变量。随机缺失(Missing at Random，MAR)指的是该类数据的缺失依赖于其他完全变量。完全非随机缺失(Missing Not at Random，MNAR)指的是数据的缺失依赖于不完全变量自身。

一般来说，缺失值的处理除了删除外，还可以采用替代法(估值法)，利用已知经验值代替缺失值。DataFrame的fillna()函数可以实现缺失值NaN的批量填充功能，格式如下:

DataFrame.fillna(value,method,inplace,...)

参数说明:value为填充值，可以是标量、字典、Series或DataFrame。method的方式有'ffill'和'bfill'这两种方式，'ffill'表示用同列前一行数据填充，'bfill'表示用同列后一行数据填充。fillna方法还可以分常数填充、字典填充两种方式。常数填充会将缺失值更换为一个指定的常数值，如fillna(n)。字典填充可以以列为单位来进行，如fillna({0∶1，1∶5，2∶10})。inplace的默认值为False，表示产生一个新的数据对象。

例3＿3＿fillna().py

对“年龄”和“体重”列有缺失值的数据进行属性分析。数据的属性分为定距型和非定距型。如果缺失值是定距型的，以该属性存在值的平均值来插补缺失的值；如果缺失值是非定距型的，则根据统计学中的众数原理，用该属性的众数(出现频率最高的值)来补齐缺失的值。经分析，同一年级学生的年龄相差不大，可以用默认值填充，而“体重”这一属性值差别比较大，属于定距型的数据，用平均值来填充比较合适。

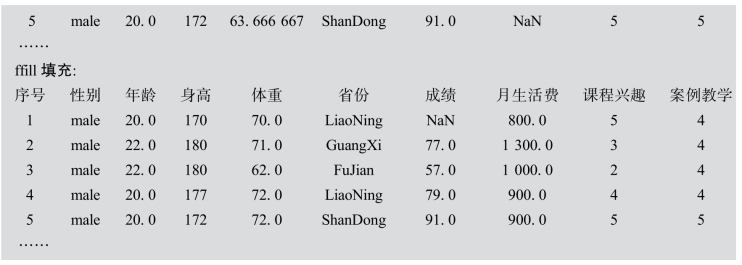
实验中，按列填充需要构造{列索引名:值}形式的字典对象作为实参。stu.fillna({'年龄':20，'体重':stu['体重'].mean()})按照字典填充方式处理后的数据如下所示，原始数据中序号为3的年龄这一属性的缺失值被填充为均值20.0，序号为5的体重这一属性的缺失值被填充为均值63.666 667。相对来说，stu.fillna(method＝'ffill')可知每个空值用上一行同列的值填充，如第五行缺失数据“年龄”被填充为上一行同列的值22.0，第五行缺失数据“体重”和“月生活费”，这两个属性值分别被填充为上一行同列的值72.0和900.0。由于部分数据结构是齐整的，如矩阵，缺失的数据会变成空值(NaN)留在其中，对后续的研究带来影响。

当缺失值的类型为随机缺失时，均值插补、同类均值插补、极大似然估计和多重插补这四种插补方法的插补效果很好。其中，均值插补和同类均值插补两种均值插补方法是最容易实现的，但是它对样本存在极大的干扰，尤其是当插补后的值作为解释变量进行回归时，参数的估计值与真实值的偏差很大。同均值插补，用层次聚类模型预测缺失变量的类型，再以该类型的均值插补。假设X＝(X1，X2，…，Xp)为信息完全的变量，Y为存在缺失值的变量，那么对X或其子集行聚类，然后按缺失个案所属类来插补不同类的均值。

相对而言，极大似然估计(Max Likelihood，ML)和多重插补(Multiple Imputation，MI)是两种比较好的插补方法。对于极大似然的参数估计常采用的计算方法是期望值最大化(Expectation Maximization，EM)，该方法适用于大样本，以保证ML估计值服从正态分布。但这种方法可能会陷入局部极值，收敛速度较慢，并且计算很复杂。多重插补的思想来源于贝叶斯估计。多重插补方法分为三个步骤:

(1)据已观测值，为每个空值估计一套可能的插补值，形成多组可选插补值。

(2)每个插补数据集合都用针对完整数据集的统计方法进行统计分析。

(3)对来自各个插补数据集的结果，根据评分函数进行选择，产生最终的插补值。与多重插补对比，极大似然估计缺少不确定成分。

案例分析1:假设有一组数据，包括三个变量Y1、Y2、Y3。它们的联合分布为正态分布，将这组数据处理成三组，A组保持原始数据，B组仅缺失Y3，C组缺失Y1和Y2。在多值插补时，对A组将不进行任何处理，对B组作产生Y3的一组估计值(做Y3关于Y1、Y2的回归)，对C组作产生Y1和Y2的一组成对估计值(做Y1、Y2关于Y3的回归)。

当用多值插补时，对A组将不进行处理，对B、C组将完整的样本随机抽取形成为m组，每组个案数只要能够有效估计参数即可。对存在缺失值的属性的分布做出估计，然后基于这m组观测值，分别产生关于参数的m组估计值，给出相应的预测，此时采用的估计方法为极大似然法，在计算机中具体的实现算法为期望最大化法(Expectation－Maximum，EM)。对B组估计出一组Y3的值，对C组将利用Y1、Y2、Y3的联合分布为正态分布这一前提，估计出一组(Y1，Y2)。由此可见，重插补弥补了贝叶斯估计的几个不足:第一，多重插补所依据的是大样本渐近完整数据的理论，在数据挖掘中的数据量都很大，先验分布将极小地影响结果，所以先验分布对结果的影响不大；第二，贝叶斯估计仅要求未知参数的先验分布，没有利用与参数的关系。而多重插补对参数的联合分布和相互关系做出估计。