如何选择合适的网格划分方法？

网格是CFD模型的几何表达形式，也是模拟与分析的载体，网格质量对CFD计算精度、计算效率以及收敛性有重要影响，因此，有必要对网格生成方式给以足够的关注。

1.网格类型

网格（grid）分为结构化网格和非结构化网格（unstructured grid）两大类。结构化网格中节点排列有序，邻点间的关系明确。而非结构化网格，节点的位置无法用一个固定的法则予以有序的命名，生成过程比较复杂，但具有极好的适应性，尤其对边界形状复杂的流场计算问题特别有效。非结构化网格需要专门的程序或软件来生成。

2.网格单元的分类

单元（cell）是构成网格的基本元素。在结构化网格中，常用的2D网格单元是四边形单元，3D网格单元是六面体单元。而在非结构网格中，常用的2D网格单元还有三角形单元，3D网格单元还有四面体单元和五面体单元，其中五面体还可分为棱锥形（或称楔形）和金字塔形单元等。下面分别给出常用的2D和3D网格单元，如图7-8和图7-9所示。

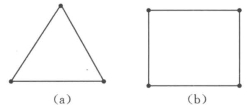
图7-8　2D网格单元图

（a）三角形；（b）四边形

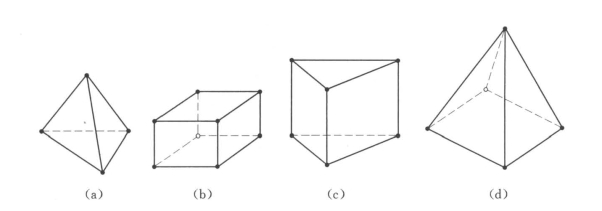
图7-9　3D网格单元图

（a）四面体；（b）六面体；（c）五面体（棱锥）；（d）五面体（金字塔）

3.生成网格的过程

无论是结构网格还是非结构网格，都需要按下列过程生成网格：

（1）建立几何模型。几何模型是网格和边界的载体，对于二维问题，几何模型是二维面；对于三维问题，几何模型是三维实体。(www.xing528.com)

（2）划分网格。在所生成的几何模型是应用特定的网格类型，网格单元和网格密度对面或体进行划分，获得网格，该步骤是生成网格的关键环节。

（3）指定边界区域。为模型的每个区域指定名称和类型，为后续给定模型的物理属性、边界条件和初始条件做好准备。

单元的形状（包括单元的歪斜和比率）对数值解的精度有着明显的影响。单元的歪斜可以定义为该单元和具有同等体积的等边单元外形之间的差别，单元的歪斜太大会降低解的精度和稳定性，如四边形网格最好的单元就是顶角为90°，三角形网格最好的单元就是顶角为60°。而比率是表征单元拉伸的度量，根据计算经验，一般应该尽量避免比率大于5∶1。

4.贴体坐标系

如果计算区域的各边界是一个与坐标轴都平行的规则区域，则可以很方便地划分该区域，快速生成均匀网格。但实际工程问题的边界不可能与各种坐标系正好相符，于是，需要采用数学方法构造一种坐标系，使其各坐标轴恰好与被计算物体的边界相适应，这种坐标系就称为贴体坐标系（body-fitted coordinates）。

使用贴体坐标系生成网格的方法的基本思想为假定如图7-10（a）所示的在x—y平面内的不规则区域，现在，为了构造与该区域相适应的贴体坐标系，在该区域相交的两个边界作为曲线坐标系的两个轴，记为ξ和η。在该物体的4个边上，可规定不同地点的ξ和η值。例如，可以假定在A点有ξ=0，η=0，而在C点有ξ=1，η=1。这样，就可把ξ—η看成是另一个计算平面上的直角坐标系的两个轴，根据上面规定的ξ和η的取值原则，在计算平面上的求解区域就简化成了一个矩形区域，只要给定每个方向的节点总数，立即可以生成一个均匀分布的网格，如图7-10（b）所示。现在，如果能在x—y平面上找出与ξ—η平面上任意一点相对应的位置，则在物理平面上的网格可轻松生成。因此，剩下的问题是如何建立这两个平面间的关系，这就是生成贴体坐标的方法。目前，常用的生成贴体坐标的方法包括代数法和微分方程法。

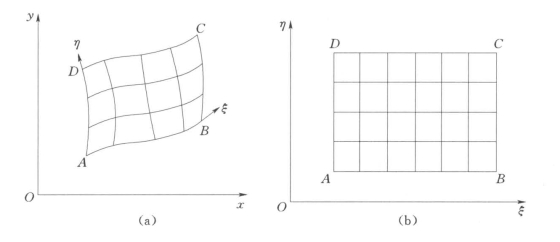
图7-10　贴体坐标示意图

（a）x—y物理平面；（b）ξ—η计算平面

5.块结构化网格

由于实际工程问题的复杂性，还有不少不规则区域中的问题难以用适体坐标方法进行求解。下面介绍的块结构化网格（block-structured grid）是另一种处理不规则计算区域问题的有效方法。这种方法从数值方法角度，又可称为区域分解法（domain decomposition method）。采用这种方法时，根据问题的条件把整个求解区域划分成若干个小的区域（块），每一个再用相应类型的网格进行离散，一般各块中的离散方程也可各自分别求解，块与块之间的耦合通过交界区域中信息的传递来实现。

采用块结构化网格的优点是：①可以大大减轻高质量网格生成的难度；②可以根据计算的需要在不同块内采用不同的网格疏密度；③便于采用并行算法来求解代数方程组。

在进行实际问题的数值计算时，网格的生成也往往不是一蹴而就的，而要经过反复的调试与比较，才能获得适合于所计算的具体问题的网格。这里包括两方面内容：①作为获得数值解的网格应当足够的细密，以至于再进一步加密网格已经对数值计算结果基本上没有影响，这种数值解称为网格独立的解；②有时需要根据初步计算的结果再反过来修改网格，使网格疏密的分布与所计算物理量场的局部率更好地相适应，这种根据计算结果而重新调整疏密分布的网格称为自适应网格。