处理动静区域问题的实用技巧

由于转子或者叶轮周期性的掠过求解域，相对惯性参考系来讲，流动是不稳定的。不过在不考虑静止部件的情况下，取与旋转部件一起运动的一个计算区域，相对这个旋转参考系（非惯性系）来讲，流动就是稳定的了，这样就简化了问题的分析。

如果除了旋转部件，静止部件也需要考虑，就不能用上述办法将问题简化。例如，在贯流泵中的转轮和导叶靠得很近，它们之间的相互作用就变得重要了。文献［Fluent］提供了以下三种解决的办法：①多参考系模型；②混合平面模型；③滑动网格模型。

MRF模型是三者中最简单的，它是不同旋转或移动速度的每个单元体的稳态近似，当边界上流动区域几乎是一致时（均匀混合），这个方法比较适宜。显然多参考系模型方法是近似的，在很多时均流的应用场合它提供了合理的模型。例如，转子和定子之间交互作用相对较弱的涡轮机可以使用MRF模型，叶轮片交互作用相对较弱，无大范围瞬态影响的混合槽可以使用MRF模型。一般来讲，由于转子和定子之间交互作用相对较弱的瞬态问题可选择MRF模型。

混合平面法中，每个流域都看成是稳态的，流域之间通过作为边界条件的混合平面上经过空间平均或者说是混合的数据来联系。通过混合就消除了流域通道之间由于周向变化而导致的不稳定（如尾流，激波，分流），从而得到稳态解。撇开混合平面模型内在的这种简化，提供了时均流场合理的近似。为理解混合平面概念，须了解混合平面模型是如何把流动区域当稳态问题来处理的。在指定的迭代间隔里，混合平面界面的流动数据是定子出口和转子入口边界数据周向平均值。采用面积—质量平均，通过做径向和轴向位置的周向平均，描述流体特性的信息就被定义了，用这些信息（径向坐标的函数，或者是轴向坐标的函数）来更新混合平面界面的边界条件。

滑动网格技术用到两个或更多的单元区域，如果在每个区域独立划分网格，则必须在开始计算前合并网格，每个单元区域至少有一个边界的分界面，该分界面区域和另一单元区域相邻，相邻的单元区域的分界面互相联系形成“网格分界面”。网格分界面应该定位在转子和定子之间的流体区域，而不能在转子或定子边缘的任何部分。在计算过程中，单元区域在离散步骤中沿着网格分界面相互之间滑动（旋转或平移）。

为了计算界面流动，在每一新的时间步长确定分界面区域的交界处，作为结果的交界面产生了内部区域（在两边都有流体单元的区域）和一个或多个周期区域。如果不是周期性的问题，那么交界面产生一个内部区域和两个壁面区域（假如两个分界面区域完全交界则没有壁面区域），如图7-6所示。重叠的分界面区域对应所产生的内部区域；不重叠的区域对应所产生的周期性区域。在这些交界面区域的面的数目随着分界面相对移动而不同，理论上网格分界面的流量应该根据两分界面的重叠处所产生的面来计算，而不是根据它们各自的分界面的面。(www.xing528.com)

在图7-7的例子里，分界面区域由A—B面和B—C面以及D—E面和E—F面组成，交叉处产生a—d面、d—b面和b—e面等。在两个单元区域重叠处产生d—b面、b—e面和e—c面而组成内部区域，剩余的a—d和c—f面成对形成周期性区域。例如，计算分界面流入Ⅳ单元的流量时，用d—b面和b—e面代替D—E面，并从Ⅰ单元和Ⅲ单元各自传递信息到Ⅳ单元。

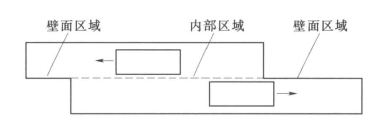
图7-6　非周期性分界面区域示意图

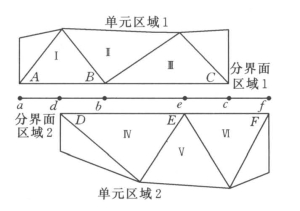
图7-7　二维分界面网格示意图

多参考系模型和混合平面模型均假设流动是稳定的，转子与定子或叶轮与轮盖的作用效果是近似的平均。这两种模型可用于转子定子之间的只有微弱的相互作用，或只需要求系统的近似解的场合；相反，滑动网格假定流动是不稳定的，因此可以真实的模拟转子定子之间的相互作用。显然滑动网格模型可用于转子和定子之间有强烈的相互作用和要求对系统进行精确的、仿真的场合，但是值得注意的是，滑动网格模型使用非稳态的数值求解，计算上的要求就相对于前两种模型要苛刻的多。