压力与速度的耦合效应

对于不可压缩流动，由于压力本身没有自己的控制方程，它是通过源项的形式出现在动量方程中，压力与速度的关系隐含在连续性方程中。求解动量方程时，一般先假定初始压力场（或上一次迭代计算所得到的结果），再由离散形式的动量方程求得速度场。压力场是假定的或不精确的，由此得到的速度场一般不满足连续方程，必须对初始压力场进行修正。由Patankar和Spalding于1972年提出的SIMPLE［46］算法成功地解决了这个问题，它修正的方法是把动量方程的离散形式所规定的压力与速度的关系代入连续方程的离散形式，从而得到压力修正方程，由压力修正方程得出压力修正值，根据修正后的压力场，求得新的速度场，然后检查速度场是否收敛，若不收敛，用修正后的压力值作为给定的压力场，开始下一层次的计算。如此反复，直到获得收敛的解。SIMPLE算法使用压力和速度之间的相互校正关系来强制质量守恒并获取压力场。

如果用猜测压力场p*来解动量方程，从连续性方程离散方程式（7-21）所得到的表面流量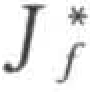为

此时满足了连续性方程，SIMPLE假定J'f写成如下形式

式中　p'——单元压力校正。

SIMPLE算法将流量校正方程［方程式（7-23）和方程式（7-24）］代入到离散连续性方程［方程式（7-19）］从而得到单元内压力校正p'的离散方程为

式中　源项b——流入单元的净流速。

压力校正方程，即式（7-25）可以用代数多重网格方法来解。一旦得到解，使用下面的方程校正单元压力和表面流动速度

式中　ap——压力亚松弛因子。

校正后的表面流速Jf在每一步迭代中一致满足离散连续性方程。

以二维为例，SIMPLE算法计算步骤如下：(www.xing528.com)

（1）假定一个速度分布，记为u0，v0，以此计算动量离散方程中的系数及常数项。

（2）假定一个压力场p*。

（3）依次求解两个动量方程，得u*，v*。

（4）求解压力修正值方程，得p'。

（5）据p'改进速度值。

（6）利用改进后的速度场求解那些通过源项物性等与速度场耦合的φ变量，如果φ并不影响流场，则应在速度场收敛后再求解。

SIMPLEC程序和SIMPLE程序相似。两种算法所使用的表达式唯一的区别就是表面流动速度校正项。和SIMPLE中一样，质量流速校正方程可写为

此时系数df重新定义为

可以看出，在压力速度耦合是得到解的主要因素时，使用修改后的校正方程可以加速收敛。