迎风格式下的二阶计算表面值方程

如果在单元的中心，如图7-1所示的c0和c1存贮标量φf的离散值，式（7-9）的对流项中需要表面值φf，因此必须从单元中心插值，这个任务由迎风格式完成。

迎风的意思就是，表面值φf是从单元上游或者说迎风处的量推导出来的，这个上游是指相对于式（7-9）法向速度vn的方向而言的，常见的几种迎风格式有一阶迎风、二阶迎风、幂率和QUICK格式。

1.一阶迎风格式

当需要一阶精度时，假定描述单元内变量平均值的单元中心变量就是整个单元内各个变量的值，而且单元表面的量等于单元内的量。因此，当选择一阶迎风格式时，表面值φf被设定等于迎风单元的单元中心值。

2.幂率格式

幂率离散格式使用一维对流扩散方程的精确解来插值变量φf在表面处的值。

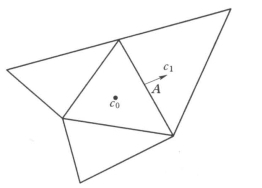
图7-1　用于显示标量输运方程离散的控制体积图

式中，Γ和ρu在间隔∂x内为一定值。积分方程（7-10）可得如下φ随x的变化关系

式中，φ0=φ|x=0；φL=φ|x=L；Pe是Peclet数。

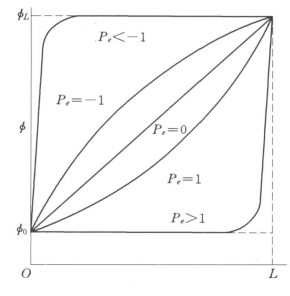
如图7-2所示为不同Pelect数下φ（x）在x=0和x=L之间的变化关系。该图表明对于较大的Pe，φ在x=L/2处的值近似等于迎风值。这就意味着当流动由对流项主导时，只需要让变量表面处的值等于迎风或者上游值就可以完成插值。

如一阶迎风格式所述，如图7-2所示，对于较大的Pe，φ在x=L/2处的值近似等于迎风值。当Pe=0（无流动或者纯扩散），图7-2表明φ可以用x=0到x=1之间简单的线性平均来实现插值。当Peclet数的值适中时，φ在x=L/2处的插值必须使用方程式（7-12）等价的幂率插值格式来得到。

(www.xing528.com)

图7-2　变量φ在x=0和x=L之间的变化［式（7-12）］图

3.二阶迎风格式

当需要二阶精度时，使用多维线性重建方法来计算单元表面处的值［5］。在这种方法中，通过单元中心解在单元中心处的泰勒展开来实现单元表面的二阶精度值。因此，当使用二阶迎风格式时，用下面的方程来计算表面值φf

式中　φ、▽φ——单元中心值和迎风单元的梯度值；

Δs——从迎风单元中心到表面中心的位移矢量。

在这种情况下需要确定每个单元内的梯度▽φ，使用散度定理来计算这个梯度，其离散格式如下

图7-3　一维控制体图

此表面处的值由邻近表面的两个单元的φ平均值来计算。最后，限制梯度▽φ以保证不会引进新的最大值和最小值。

4.QUICK格式

对于四边形和六面体网格，可以确定它们唯一的上游和下游表面以及单元，如图7-3所示。QUICK类型的格式［133］是通过变量的二阶迎风与中心插值加上适当的权因子得到的，具体可以写成

在式（7-15）中θ=1就是中心二阶插值，θ=0就是二阶迎风值。传统的QUICK格式对应的θ=1/8。当结构网格和流动方向一致时，QUICK格式明显具有较高精度。