贯流泵机组起动过渡优化方案

贯流泵站扬程虽然较低，但流道短且直，泵机组起动时，水泵扬程极易迅速升高，因而水泵水力矩在起动后较短时间内就出现较大值，很可能使水泵机组总阻力矩在电动机起动加速至某种转速时达到或大于电动机瞬时起动转矩，致使电动机超载，泵机组不能正常起动，因此有必要适当加大电动机超载系数λ。在设计贯流泵站时适当加大出水侧水体容积，能够保证在机组起动时泵装置扬程不致增加太快、太大，可以使泵安全起动。对于已建成的贯流泵站，如淮安三站，当出水侧容积较小时，通过在快速闸门上设置分流小拍门是一种满足安全溢流要求、减小泵装置扬程增加太快、太大的有效措施。

贯流泵出水侧通常有两种结构形式，如图4-3所示，图4-3（a）为胸墙溢流、快速闸门启门；图4-3（b）为胸墙溢流、小拍门分流、快速闸门启门。下面建立起动过渡过程的数学模型。

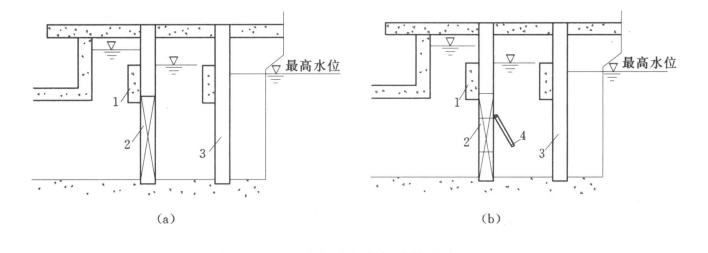
图4-3　贯流泵出水侧结构形式

（a）胸墙顶部溢流；（b）胸墙溢流、小拍门分流1—胸墙；2—快速闸门；3—检修门；4—小拍门

1.力矩平衡方程

水泵机组起动过程中的力矩平衡方程为

式中　MD——电动机电磁力矩，N·m，按式（4-1）计算；

J——水泵机组转动惯量，N·m2；

MZL——总阻力矩，N·m。

总阻力矩M2L包括水泵水力矩M、水泵惯性附加力矩MG、推力轴承摩擦力矩MC、电动机风扇阻力矩MF、电动机转子风阻力矩Mz、油黏滞阻力矩MN与径向轴承摩擦力矩MΔ等，其中

（1）水泵惯性附加力矩

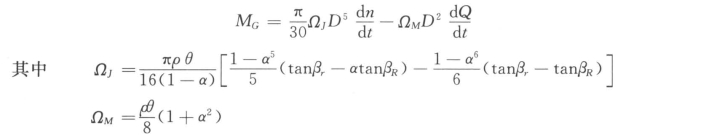
式中　θ——泵叶片平面包角，rad；

α——泵叶轮轮毂比；

βr——叶片根部翼型安放角，（°）；

βR——叶片外缘翼型安放角，（°）。

（2）推力轴承摩擦力矩

式中　H——水泵扬程，m；

f——动压摩擦系数，一般f=0.05；

kp——系数，kp取0.9～1.0；

r——推力头当量摩擦半径，m。

（3）电动机风扇阻力矩MF=f1n2，f1为常系数。

（4）电动机转子风阻力矩Mz=f2n，f2为常系数。

（5）油粘滞阻力矩MN=f0n，f0为常系数。

（6）径向轴承摩擦力矩MΔ，与泵机组转动部件重量、径向轴承半径有关，若假定动摩擦系数为常数，则MΔ为常数。

于是，式（4-14）为：

当n＜0.95nr时

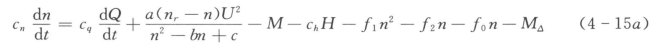
当n≥0.95nr时

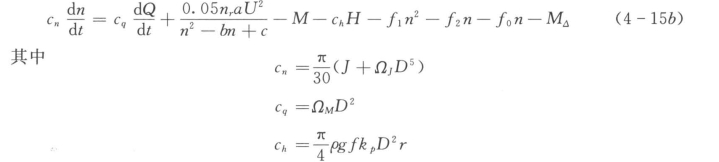
对式（4-15a）与式（4-15b）在微小时间段Δt内积分，并利用式（4-5）～式（4-7），可以得到力矩平衡表达式：

当n＜0.95nr时

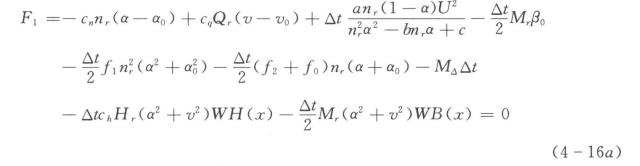
当n≥0.95nr时

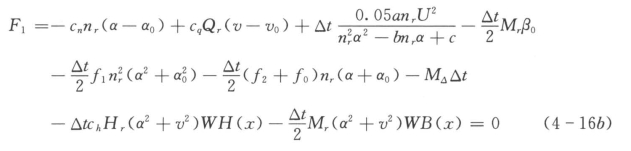
2.水头平衡方程

利用刚性水锤概念列写水头平衡方程。

（1）胸墙顶部溢流情形：

当▽P≤▽W时

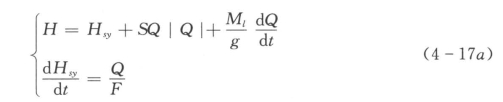
当▽P＞▽W，胸墙顶部出现溢流，则有

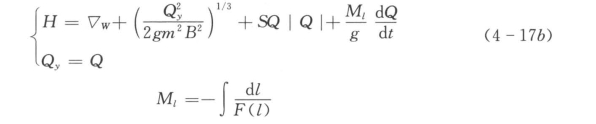
式中　▽P——流道出口出水池水位，▽P=▽in+Hsy，▽in为进水池水位；

▽W——胸墙顶部高程，m；

Hsy——装置扬程，m；

F——流道水平截面积；

S——流道阻力参数，s2/m5；

Q——泵流量，m3/s；

F（l）——垂直于流道中心线流道各断面积的流道长度函数；

l——沿流道中心线长度；

Qy——胸墙顶部溢流量，m3/s；

m——胸墙顶部溢流流量系数；

B——胸墙顶部溢流宽度，m。

对式（4-17a）与式（4-17b）在微小时间段Δt内积分，并利用式（4-5）～式（4-6），可以得到水头平衡方程式：

当▽P≤▽W时

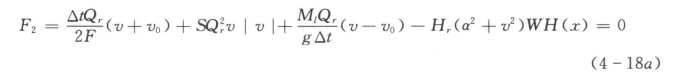
当▽P＞▽W时

（2）快速闸门上小拍门分流、胸墙顶部溢流情形：

当▽P≤▽W时(www.xing528.com)

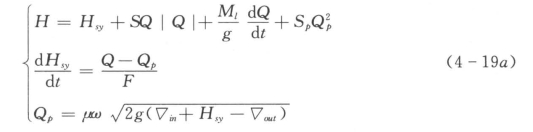
当▽P＞▽W时

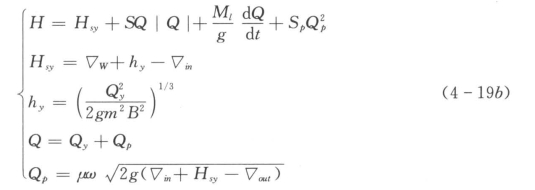
式中　Qp——小拍门的泄水流量，采用孔口出流公式计算；

μ——小拍门孔口出流流量系数；

ω——小拍门孔口面积；

▽out——快速闸门外出水池水位；

Sp——小拍门孔口阻力参数，s2/m5；

其他参数含义同上。

对式（4-19a）与式（4-19b）在微小时间段Δt内积分，并利用式（4-5）～式（4-6），有：

当▽P≤▽W时

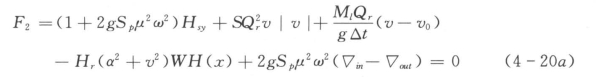
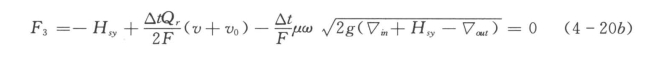
当▽P＞▽W时

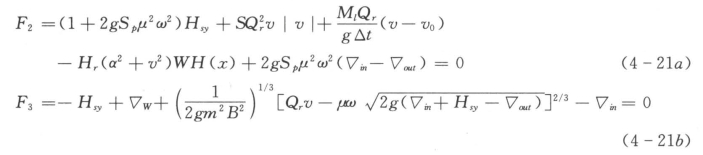
3.起动过渡过程求解

分胸墙顶部溢流与快速闸门上小拍门分流、胸墙顶部溢流两种情形讨论。

（1）胸墙顶部溢流情形。贯流泵起动过程可以用式（4-18a）、式（4-18b）以及式（4-16a）、式（4-16b）组成的以α，v为自变量的方程组来描述。

计算的初始条件为：t=0时，H=Q=Hsy=n=0。

用Newton-Raphson迭代法求解上述方程组，即

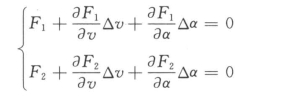
其中当n＜0.95nr时

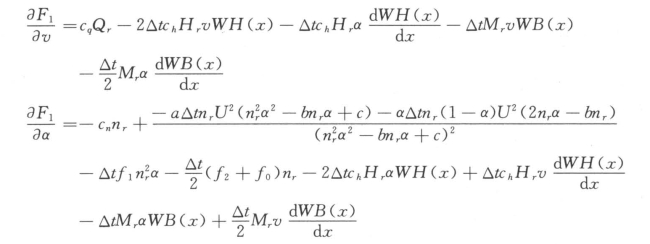
当n≥0.95nr时

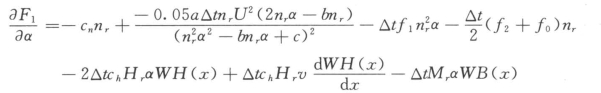
当▽P≤▽W时

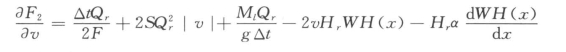
当▽P＞▽W时

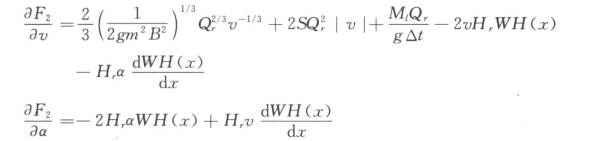
迭代求解的步骤如下：

1）根据计算时段的初始值v0、α0和前一个计算时段的初始值v00，α00线性外插初定v和α值：v=2v0-v00，α=2α0-α00。

2）计算偏导数值，再计算F1和F2值。

3）计算修正值

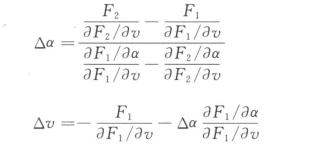
4）若第k次迭代算出的修正值为Δαk和Δvk，则在开始进行第K+1次迭代时，应使αk+1=αk+△αk；vk+1=vk+Δvk。

5）如此循环迭代，直到满足下列条件时为止

式中　ε——设定的微小数，例如0.0002。

6）转入下一计算时段的运算。

（2）快速闸门小拍门分流、胸墙顶部溢流情形。贯流泵起动过程可以用式（4-20a）、式（4-20b）、式（4-21a）、式（4-21b）以及式（4-16a）、式（4-16b）组成的以α，v，Hy为自变量的方程组来描述。计算的初始条件为：t=0时，H=Q=Hsy=n=0。

用Newton-Raphson迭代法求解上述方程组，即

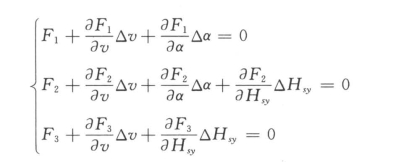
当n＜0.95nr时

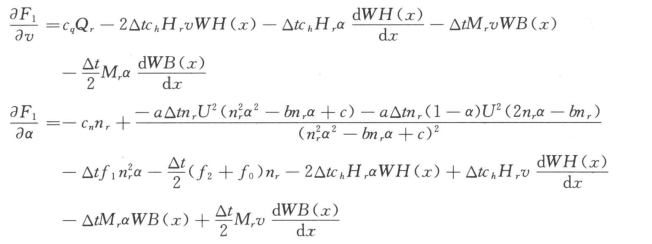
当n≥0.95nr时

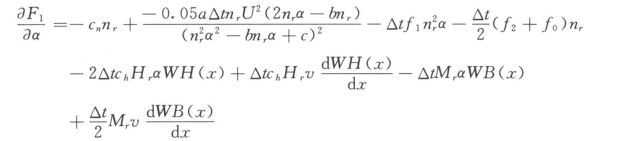
当▽P≤▽W时

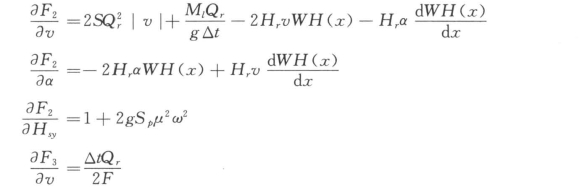
当▽P＞▽W时

当▽P≤▽W时

当▽P＞▽W时

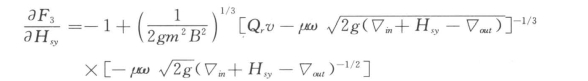
迭代求解的步骤如下：

1）根据计算时段的初始值v0、α0、Hsy0和前一个计算时段的初始值v00、α00、Hsy00线性外插初定v、α、Hsy值v=2v0-v00，α=2α0-α00，Hsy=2Hy0-Hsy00。

2）计算偏导数值，再计算F1、F2和F3值。

3）计算修正值

式中　ε——设定的微小数，例如0.0002。

6）转入下一计算时段的运算。