翼型几何参数与动力特性

如图3-1所示的贯流式叶轮，用任意半径r及r+dr的两个同心圆柱面截取一个微小圆环柱层，将圆环柱层沿母线切开，展开成平面，形成厚度为dr的翼型系列，构成一组由相同翼型等距排列的平面直列翼型系列，称为平面直列叶栅。因此，贯流式叶轮内的流动就简化为平面直列叶栅的绕流问题。

这组叶栅具有如下特点：

（1）可以在平面上展开，即为平面叶栅。

（2）叶栅列线（栅中翼型各相应点的连线）为直线，即为直列叶栅。

（3）栅中翼型的间距相等，液体绕流每个翼型的作用相同，没有边界翼型，即为无限叶栅。

所以，这组叶栅是无限平面直列叶栅，叶栅中每个翼型的绕流情况相同，只要研究绕流叶栅中一个翼型的绕流，就可推广到整个叶栅的流动分析，研究贯流泵叶轮内的流动就简化为研究对应几个圆柱流面上叶栅中翼型的绕流问题。

1.翼型及其主要的几何参数

机翼叶片的横截面称为翼型，它具有确定的几何型线和空气动力学特性。翼型的主要几何参数，如图3-5所示。

（1）中线。通过翼型内切圆的圆心的连线，又称为翼型骨线。

（2）前/后缘点。中线与型线的交点，前端称前缘点，后端称后缘点。

（3）翼弦l。连接前缘点与后缘点的直线，其长度称为弦长。

（4）翼展b。垂直于翼型方向的叶片长度（机翼的长度）。

（5）展弦比λ。翼展b与弦长l占之比。

（6）挠度f。弦长到中线的距离，最大距离称最大挠度。

（7）厚度c。翼型上、下表面之间的距离，最大值称为最大厚度。

（8）冲角α。翼型前来流速度方向与翼弦的夹角，冲角在翼弦以上时为正冲角，在以下时为负冲角，如图3-6所示为正冲角。

（9）前/后驻点。来流接触翼型后，开始分离的点（此点速度为零）为前驻点；流体绕流翼型后汇合的点（此点速度也为零）为后驻点。前驻点和后驻点不一定与前缘点和后缘点重合。

（10）前缘圆角半径RL。翼型前缘的曲率半径。

（11）后缘角τ。翼型后缘处上、下翼线切线的夹角。

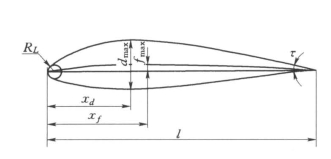
图3-5　翼型的几何参数图(www.xing528.com)

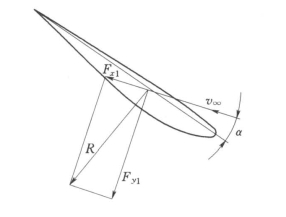
图3-6　作用于翼型上的力图

2.翼型的空气动力学特性

翼型的空气动力学特性是指翼型升力和阻力特性与翼型几何形状、冲角及流动参数的关系。

流体绕流翼型时，在翼型上产生垂直于来流方向的升力Fy1和平行于来流方向的阻力Fx1，如图3-6所示。

升力和阻力分别用式（3-14）计算

式中　cy1——翼型升力系数；

cx1——翼型阻力系数；

ρ——流体密度，kg/m3；

l——弦长，m；

b——翼展，m；

v∞——无限远处未受扰动流体的速度，m/s。

（1）升、阻力系数曲线。升力系数外cy1和阻力系数cx1与翼型的几何形状及冲角有关。对于各种翼型的cx1和cx1值，均由风洞试验求得，并将试验结果绘制成cy1和cx1与冲角α的关系曲线，这种曲线称为翼型的空气动力学特性曲线，如图3-7（a）所示。

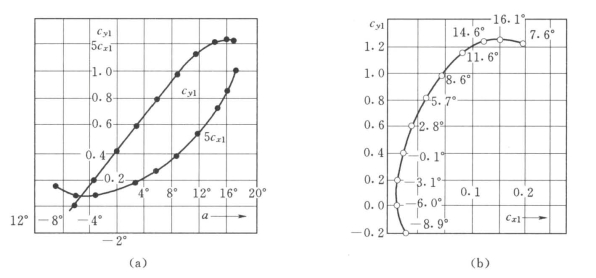
图3-7　空气动力特性图

（a）翼型空气动力学特性曲线；（b）翼型的极曲线

由图3-7可以看出，升力系数cy1随冲角α的增大而增大，当α超过某一数值时，升力系数cy1下降。这是因为此时的流体在后缘点前发生附面层分离，在翼型后面形成很大的旋涡区，使翼型上下表面的压差减小所致。升力系数减小的点称为失速点，冲角增大到失速点后，空气动力学特性就大为恶化，在贯流式泵中失速工况将使性能恶化，效率降低，并伴随着有噪声及振动现象。

过原点作极曲线的切线，其切点所对应的冲角，就是最佳冲角（与ε最大值对应的冲角）。

作用在翼型上的合力F与升力Fy1之间的夹角称为升力角用符号λ表示。λ越小，则升力越大而阻力越小，翼型的空气动力特性越好。对每种翼型，都对应一个最小的λ角。