煤岩蠕变损伤理论模型的优化

通过前述Burgers蠕变模型与H-K蠕变模型的对比分析，得出Burgers蠕变模型可以很好地反映煤岩在较低应力状态下（小于长期强度或者小于屈服强度）的瞬时弹性应变、衰减蠕变以及稳态蠕变，但不能反映煤岩在高应力状态下的加速蠕变阶段。因此，有必要在Burgers蠕变模型的基础上建立一种能描述煤岩在荷载作用下反映煤岩蠕变全过程的损伤本构模型。

关于煤岩时效损伤的应力阈值问题，目前有两种主要观点：一种认为损伤不存在阈值，损伤随着应力即时产生；另一种观点认为煤岩蠕变损伤的应力阈值为煤岩的长期强度，即应力水平大于长期强度时，煤岩会随着时间产生损伤。实际上，损伤产生于加速蠕变阶段，损伤应力阈值与煤岩的长期强度一致。当煤岩所承受应力大于长期强度时，煤岩在有限的时间内发生破坏。而当煤岩所承受应力小于长期强度时，永远不可能使之发生蠕变破坏。

在粘塑性本构理论的研究方面成果比较多，Chaboche在1979年提出了考虑非线性运动硬化（蠕变第三阶段）的粘塑性模型，该模型主要应用在材料的破坏方面。Chaboche模型有多种表述形式，在不考虑热应变的前提下，应变可分解为：

式中，ε为总应变，εe为弹性应变，εi为非弹性应变。在小变形情况下：

Chaboche模型中引入了损伤变量D和等效应力σeff，等效应力是由于损伤存在而产生的。在含瓦斯煤卸围压蠕变试验中，考虑瓦斯压力G形成的孔隙压力，有效应力可按下式表述：

令D为各向同性本构张量，根据广义胡克定律，有：

则弹性部分的应变与应力有如下关系：

损伤演化采用Rabotnov定律描述为：(www.xing528.com)

式（5.39）中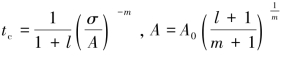，，l为Rabotnov补充系数，m与A0为蠕变损伤系数，t为试验时间，tc为试件断裂时间。

假定试件破坏时的损伤变量Dc＝0.1，即可根据不同试验确定损伤变量D中的各参数。

式（5.34）中非弹性（粘塑性）部分的应变可由考虑损伤的Chaboche模型确定：

式（5.40）中，Seff是由等效应力定义的偏应力；x用来描述材料的硬化，称为背应力；R为各向同性硬化函数，用于描述材料各向同性硬化能力的变化；〈〉为MacCauley括号，J2为第二不变量；f（Seff，x，R）是屈服函数。

式（5.41）中，k为材料参数，J2可按下式求解：

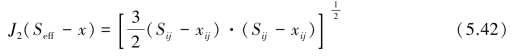
因此，通过试验可以确定模型中的l、m、x、R、k相关参数，图5.3为理论模型与试验曲线的对比，表明考虑瓦斯压力的Chaboche模型可以模拟卸压蠕变的总体硬化过程。

图5.3　理论模型与试验曲线对比