煤岩粘弹性蠕变模型分析

仔细分析煤岩、砂岩以及灰岩等煤岩试样的单轴压缩以及三轴压缩蠕变试验曲线不难发现，在低于某一荷载水平（即未出现加速蠕变荷载）之前煤岩的蠕变试验曲线具有如下几个特征：

①在施加应力以后，煤岩立即产生瞬时弹性应变，可知蠕变模型中应包含弹性元件；

②煤岩蠕变应变随时间的增加而有增大的趋势，可知蠕变模型中还应包含粘性元件；

③在一定应力水平下，随时间推移，应变有保持某一稳定数值的趋势。

因此，可以得出煤岩在未出现加速蠕变荷载作用下表现为典型的粘弹性特征。可以描述煤岩粘弹性蠕变特征的蠕变模型有表5.1所示的H-K模型（三元件广义Kelvin模型）、Burgers模型、Bingham模型以及西原模型等。H-K模型与Burgers模型的参数少，便于参数识别与进一步扩展研究，因此这里选用H-K模型（三元件广义开尔文模型）与Burgers模型对煤层裂隙场涉及的煤岩、砂岩、灰岩等蠕变试验曲线进行辨识分析。

1）H-K模型

H-K模型是由弹性元件（H）与开尔文模型（K）串联的结构模型，通常也称为三元件广义Kelvin模型，如图5.1所示。

图5.1　三元件广义Kelvin模型

该模型所受的总应力σ和总应变ε的关系为：设H体应力为σ1、应变为ε1以及K体应力为σ2、应变为ε2。该模型串联的特点是应力相等而应变相加。因而有：

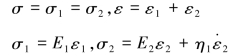
从以上方程式中消除σ1、ε1、σ2、ε2，即可得到H-K模型的蠕变本构关系：

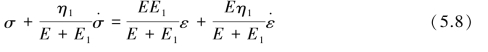
或

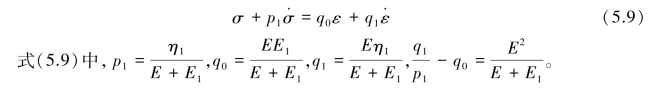
三维张量方程为：

式（5.8）、式（5.9）与式（5.10）均为H-K模型的本构方程式。

（1）H-K模型的蠕变

应力条件为：S′＝S′0＝恒量，初始条件为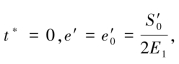：由本构方程（5.10）可得：

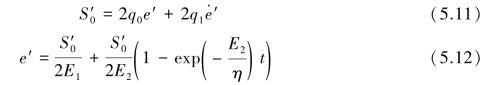
式（5.11）、式（5.12）便为H-K模型的蠕变方程。弹性模型1可以有瞬时弹性变形，而弹性模型2因粘壶的限制而不能发生瞬时变形。当∞，则应变随着时间的增加呈指数形式递增，最终得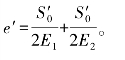

（2）H-K模型的松弛

应变条件为e′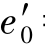＝＝恒量，初始条件为：t*＝0、S′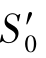＝，由本构方程（5.10）可求得松弛方程为：

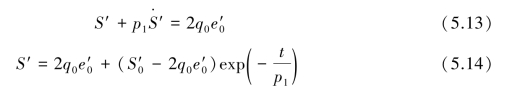
将式（5.14）转化为：

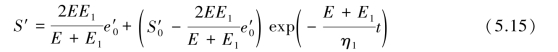
式（5.14）、式（5.15）均为H-K模型的松弛方程。当t*＝0，S′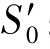＝；当t*→∞，在经历极长时间后，则应力降低到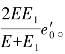

2）Burgers模型

Burgers模型是由马克思威尔模型（M体）与开尔文模型（K体）串联组合的结构模型（图5.2）。

图5.2　Burgers模型(www.xing528.com)

设马克思威尔模型与开尔文模型应变分别为ε1、ε2，串联后总的应变为两个应变相加，而应力相等，故有：

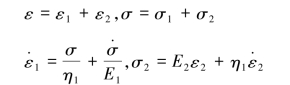
将上述方程式中消去ε1、ε2，即可得到Burgers模型的蠕变本构关系：

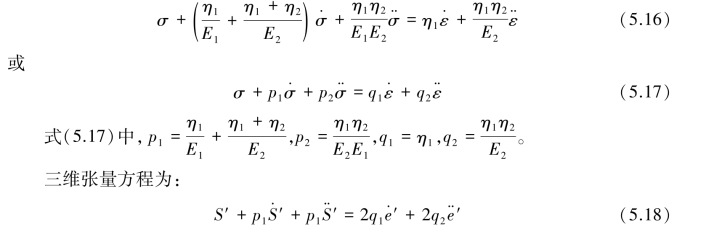
式（5.16）、式（5.17）与式（5.18）均为H-K模型的本构方程式。

应力条件为：S′＝＝恒量，初始条件为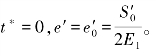：这里应用拉普拉斯（Laplace）变换进行蠕变方程的推导，对于瞬时加载时间引入一个单位阶梯函数Δ（t），其定义为：

因而，应力S′可表示为：

应变e′的拉普拉斯变化为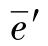，e′的导数的拉普拉斯变换为：

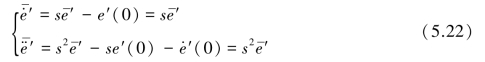
对三维本构方程式（5.18）进行拉普拉斯变换，以及将式（5.21）与式（5.22）代入式（5.18），得：

式（5.25）即为Burgers蠕变方程，将p1、p2、q1、q2代入可得：

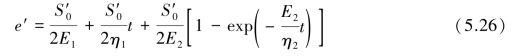
Burgers蠕变模型描述介质具有初始瞬时弹性应变、衰减蠕变（Ⅰ）阶段以及稳态蠕变（Ⅱ）阶段。

3）参数识别以及对比分析

目前，煤岩蠕变模型参数确定的方法多为回归反演法、最小二乘法以及蠕变曲线分解法等。其中，最小二乘法应用最为普遍，但最小二乘法解决非线性问题的效果并不理想。因此，本项目采用quasi-Newton算法（BFGS算法）对煤岩蠕变模型进行参数识别。

BFGS算法是由Broyden、Fletcher、Goldfarb和Shanno等人在1970年提出的。该算法不用计算二阶偏导数矩阵及其逆阵就可以构造出每次迭代的搜索方向。该算法数值稳定性好，可直接对蠕变全过程曲线拟合，故BFGS算法被认为是目前最好的一种局部收敛算法，得到了极为广泛的应用。其搜索方向的构造如下：

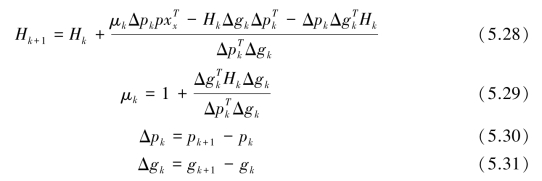
式中，k为迭代次数。计算步骤如下：

①给定迭代初始值。初始为p（0），设定计算精度ε＞0，初始矩阵H0＝I（单位矩阵），令k＝0。

②搜索和迭代。计算s（k）＝－Hk gk，沿s（k）进行不精确一维搜索，求出步长λk，使

③执行熟练准则。若‖gk＋1‖＜ε，则取p*＝p（k＋1），计算结束；否则，由式（5.27）～式（5.29）计算Hk＋1，令k＝k＋1，返回步骤②。

在压缩作用下，H-K蠕变模型以及Burgers蠕变模型与试验曲线的吻合度均比较好，且二者相比，Burgers蠕变模型与试验曲线的吻合度更高；然而，对于煤岩直接拉伸蠕变试验，Burgers蠕变模型与试验曲线的吻合度明显高于H-K蠕变模型。这是因为Burgers蠕变模型较H-K蠕变模型多了一个粘性元件，因而，其更适用于较为复杂的受力状态，表5.2、表5.3所示为两个模型的拟合参数。

表5.2　Burgers蠕变模型参数

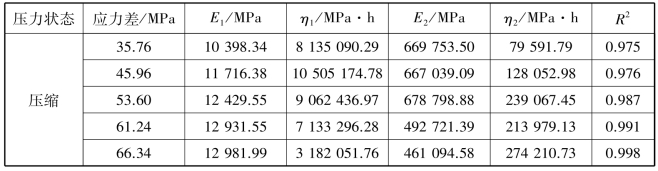
表5.3　H-K蠕变模型参数

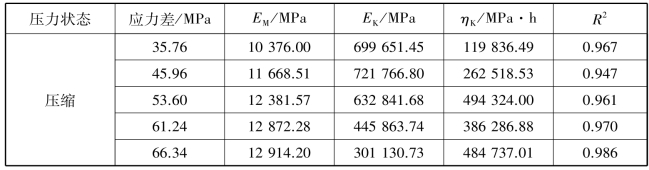
根据表5.2、表5.3可知，拟合相关系数平方（R2）均在0.9以上，最高达到了0.998，说明拟合效果相当好，且在应力状态相同的情况下，Burgers蠕变模型各项拟合相关系数平方（R2）均明显高于H-K蠕变模型。同时可以看出相同荷载作用下，各参数的变化范围相对较小。