静电偏转控制系统的控制方法及应用

利用垂直于电子束运动方向的静电场使电子束改变方向，发生偏转的电子光学系统称为静电偏转系统［14］。其中最简单的一种是平行板静电偏转系统［14-15］，如图12-5 所示。

设两平行板间的电压为2U，间距为d，若忽略边缘效应，可以认为平行板间的电场是沿y 方向的均匀场，对从其中心平面（y=0）平行于z 轴入射的电子计算其轨迹，不难得出在偏转板出口处y 方向的偏转量为

式中：a 为偏转板长度；Ua 为加速电压。电子在偏转板出口处的偏转角正切为

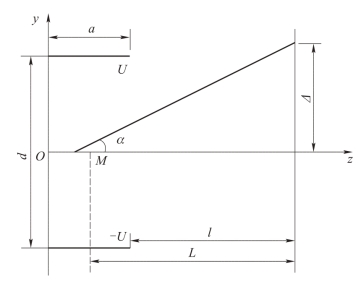
图12-5　平行板静电偏转系统

在目标处的偏转量为

(www.xing528.com)

其中l 为偏转板出口至目标的距离，这一段距离为无场空间。其中电子轨迹为直线。将该直线向后延长交z 轴于M 点。从目标向后看去，好像电子是从M 点以α 角偏转过来的，M 点称为偏转中心。由式（12-17）及式（12-18）可知M点恰好在偏转板中心。因此目标处偏转量可以写成

其中L= a/2 + l 为偏转中心至屏的距离。

偏转灵敏度εe 定义为单位偏转电压产生的偏转量，即

通常以mm/V 为单位。上式表明静电偏转灵敏度与电子荷质比无关，并反比于加速电压。静电偏转系统的基本问题是提高灵敏度、减少偏转像差并增加偏转信号的频宽（当偏转信号是交变场信号时）。

设计静电偏转系统时，要考虑到提高偏转灵敏度、增大偏转角和减少偏转像差等方面的要求。对于平行板，在一定的偏转电压2U 和加速电压Ua 下，为提高灵敏度可加长偏转板长度a 及减少板间距离d。但这些与增大偏转角的要求相矛盾，因为最大偏转角αmax ≈d/e。因此只有改变偏转板的形状，使偏转板按电子轨迹形状弯曲才能同时达到高灵敏度和大偏转角。麦洛夫（Maloff）和爱泼斯坦（Epstein）曾计算出这种弯曲板的数学表达式。但由于加工及安装困难。实际上常用多折板近似地代替弯曲板。其偏转灵敏度可达到弯曲偏转板的95%。

上述讨论中我们假定了偏转场是理想的均匀电场。这时不论被偏转的电子束从场的中心还是边缘通过，束斑的大小都保持不变，且偏转量正比于偏转电压。这种情况称为理想的高斯偏转。但实际的偏转场不可能为理想的均匀电场，所以只有在偏转角小时才能实现理想的高斯偏转；当偏转角较大时会出现与高斯偏转的偏离，这就是偏转像差［14］。偏转像差会增加电子束方向控制的难度，不利于电子束的束形控制。