空间碎片的降轨模式及原理分析

为了便于讨论高能电子束进行碎片清除的机理和可行性，这里首先对空间碎片降轨清除的基本原理、降轨模式进行简要的介绍。

1.降轨清除判据

一般认为，空间碎片在降轨再入大气层的过程中，当其轨道高度降至130 km时将在大气阻力的作用下逐渐烧毁［43-44］。为了节省能量、提高清除效率，在设计碎片降轨的最终轨道时，可充分利用空间碎片再入大气层的自然降轨过程，适当提高最终轨道的近地点高度。为了估算碎片自然降轨所需的时间，以圆轨道为例。空间碎片运动一圈时高度的变化Δr 为［45］

式中：r 为空间碎片的初始轨道高度；CD 为阻力系数，在200～500 km 的范围内为2.2～2.5；ρ 为大气密度；S 为有效阻力面积。

初始轨道高度为r 的碎片在烧毁之前需要运行的圈数n 为

碎片的运行周期T 为

式中：a 为轨道的半长轴；μ 为地球引力常数，其值为3.986 × 105 km3/s2。通过自然降轨逐渐烧毁所需的时间为t= nT。以运行在高度为200 km 的圆轨道、半径为5 cm 的铝球为例，其通过自然降轨逐步烧毁所需的时间为7 d 左右。考虑到降轨时间和效率，可选择h=200 km 的圆轨道作为空间碎片降轨清除的判据。

2.常用变轨方案

当前的碎片降轨清除中，较为常见的当属霍曼转移和单脉冲共面变轨。下面分别对这两种变轨方案进行简要的介绍。

1）霍曼转移

霍曼转移是指两个同心圆轨道之间的转移，主要用于清除为特定区域内的空间碎片，部分近圆轨道空间碎片的降轨过程也可视为霍曼转移。采用霍曼转移可以估算特定区域内空间碎片清除所需的激光或高能电子束能量，为激光器或电子束系统的参数设计提供依据。霍曼转移过程如图11-16 所示。

激光或电子束在A 点辐照空间碎片后，产生的速度增量使碎片沿长轴为r1 + r2 的椭圆转移轨道运行，当碎片运行到高度为200 km 时再入大气层烧毁。

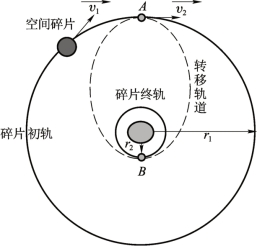
图11-1　6 霍曼转移过程(www.xing528.com)

碎片在初始轨道上的运行速度v1 为

在转移轨道上A 点处的速度v2 为

所需要的速度增量为

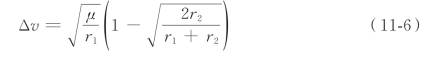
2）单脉冲共面变轨

单脉冲共面变轨是指两个共面且相交的轨道之间的变轨方案，一般针对特定空间碎片的轨道，主要用于在已知激光器或电子束系统参数的情况下，确定碎片降轨过程的轨迹和所需的时间，为激光或高能电子束作用于碎片的时间和作用点位置的确定提供依据。单脉冲共面变轨过程如图11-17 所示，碎片在初轨A 点处的速度v1，其大小为

式中：r 为A 点的轨道高度；a1 为初轨的半长轴。

变轨后碎片在最终轨道A 点处的速度为v2，其大小为

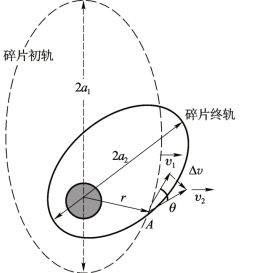
图11-1　7 单脉冲共面变轨过程

式中：a2 为终轨的半长轴。则变轨所需的速度增量大小为