如何调整三频率法耦合器的尺寸？

耦合器［15-16］是行波电子直线加速管的重要组成部分，用以实现标准矩形波导与标准加速腔间的阻抗匹配，以及所传输电磁场的波形转换，使微波功率能以尽可能小的反射馈入加速管，或将加速管的剩余功率耦合到与输出波导相连接的干负载。常见的单边耦合器为一个顶部开矩形耦合孔的腔体，与后面的加速结构同轴连接，因此也常称之为耦合腔。耦合腔的设计过程较为烦琐，三频率法为当前的一种主流设计方法。

1.三频率法

三频率法（也称Kyhl 方法）是美国SLAC 国家加速器实验室的Westbrook于1963 年提出的，当时主要用来调配电耦合的2π/3 模行波加速管耦合器。该方法要求事先已知加速腔链的色散频率fπ/2、f2π/3 及fmean= （ fπ/2 + f2π/3）/2，还要求耦合器后连接一小段加速腔链，且这一小段腔链可以是未完全调配好的腔链。用该方法调配耦合器主要遵循以下步骤。

（1）使用短路活塞失谐耦合腔，确定输入波导中与相应频率fπ/2、f2π/3（加速管的工作频率）以及fmean 对应的失谐短路参考面。

（2）将短路活塞移动到与耦合腔相邻的腔中心面，使该腔失谐。

（3）调整耦合腔的腔体尺寸，以使与频率fmean 对应的反射相位在Smith圆图上相对于失谐短路参考面顺时针移动1/4 个波长，即180°。如果移动的距离小于1/4 个波长，则表明耦合腔的谐振频率偏低于f2π/3，反之，则偏高于f2π/3。

（4）保持短路活塞的位置不变，测量与频率fπ/2 和f2π/3 对应的反射相位在Smith 圆图的位置。如果耦合度β 为1，则此时各个数据点在Smith 圆图上的位置如图7-7 所示。由于耦合器的耦合腔在调配前一般处于欠耦合状态，各个数据点在Smith 圆图上的实际位置将有所偏离。

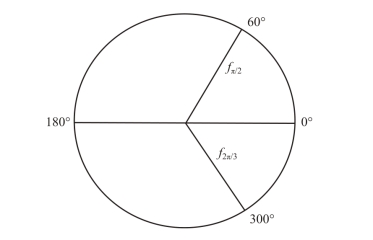
图7-7　使用三频率法调配耦合器时的Smith 圆图

（5）调整耦合孔的尺寸，对其进行修整后，测量并记录修整好的尺寸。调整耦合孔的尺寸将会对耦合腔的频率有所影响。

（6）重复步骤（3）、（4）、（5），直到耦合度等于1 为止，此时，对耦合器的调配即告完成。

1993 年，法国的Chanudet 把三频率法推广到任意模式的电耦合或磁耦合的行波加速结构，其结论为：失谐耦合腔并假设所有频率的输入反射相角都为0°，则移动活塞到相邻腔的中心面，并测量输入波导中三频率fπ/2 和fθ（加速管的工作频率）以及fmean 对应的反射相位φπ2、φθ 及φmean，则当耦合器匹配时，满足表7-3 所示关系［15］。

表7-3　不同工作模式对应的反射相位

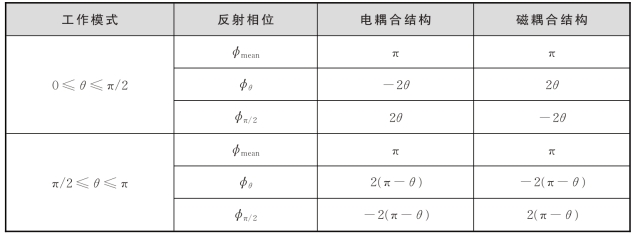
上述三频率法都只能定性判断耦合器频率偏差Δf（耦合腔的实测频率与设计频率的差）的高低及输入耦合度β 的强弱，不能定量地计算Δf 以及β 值。郑署昕等在Chanudet 的基础上对三频率法测量耦合器做了定量分析，给出了定量判断Δf 以及β 的方法。用该方法，只需要知道任意两个频率的测量数据（频率f、反射相位），就可近似计算耦合器在工作模式处的耦合度和频偏Δf，其计算公式为［15］

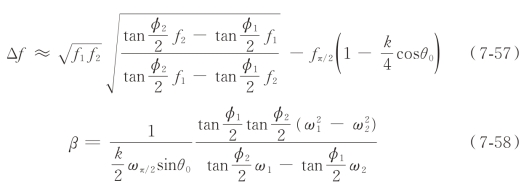
其中，k 为相邻腔间的耦合系数，可以由加速腔链的色散方程fθ= fπ2（1 -kcosθ/2）计算得到。

2.基于CST 软件的耦合器设计

耦合器的设计在前人的工作基础上，已经由最初的试验探索性方式发展到现在的利用快速的计算机模拟软件的方法。试验探索方法需要研究人员具有丰富的经验，耗时耗力效果还不好。电磁模拟软件的发展和应用为耦合器的设计、调配提供了极大的便利。在早期常应用基于MAFIA3D 时域求解器的调节方法，但此种方法在3D 建模时有缺陷，尤其是在复杂的模型上。建立在有限元基础上的CST 微波工作室相比MAFIA3D 有更为友好的用户界面，使初学者较易掌握，尤其是其PBA （Perfect Boundary Approximation，完美边界近似）和TST （Thin Sheet Technology，薄板技术）功能使得用户在较小的网格划分中得到满足误差范围内的结果，这样就为研究节省了很多时间，而且C S T 中的时域和本征模求解器可以在调配过程中相互佐证，确保了调节结果的正确性。本小节重点介绍在三频率法的基础上如何应用C S T 软件调配耦合器。

对于一个设计、调配好的耦合器应该具备以下两个条件：第一，它能与标准的矩形波导相匹配，起到波形转换的作用，并且将功率源中的功率最大效率地馈入加速管中，这一目标通过调节耦合孔的尺寸来实现；第二，它必须工作在谐振频率下，使得单元腔相移和场分布均符合要求，这一点只需通过调节耦合腔的内径。在耦合器调配的过程中，给定一个初始的耦合孔的高度值t，只要调节耦合孔的宽度h 和内半径b 值就可以，最终确定满足以上两个条件的耦合器的尺寸。在计算中，先确定在满足误差范围内的网格划分，以便在以下所有的计算中统一网格。具体计算步骤如下［17］。

（1）在三频率法中调配耦合器，计算加速单元在三个不同相移条件下的谐振频率fπ/2、f2π/3 以及fmean，这在之后的调节中是很重要的参数。通过本征值求解器求解单个盘荷单元的谐振频率如表7-4 所示。

表7-4　三频率法中的谐振频率GHz

（2）根据经验给出初始的b 和h 值，建立如图7-8 所示模型，输入波导L 值应足够大，以使得包含所有的失谐段路面。在MWS 中将短路金属棒端部放在耦合腔的中心位置（不同的加速结构金属棒的位置有所偏差），使耦合器失谐。设定输入波导末端的边界条件为电边界，利用MWS 中本征模求解器的频率扫描功能，扫面随L 值变化的本征模频率，找出耦合器的谐振频率满足f=fmean 的L 值，此时波导长度记为Lmean。可以直接用MWS 中的频域快速求解器求解S11 参数求得L 值，如图7-9 所示，当fmean 对应的相位小于180°时，减小L 值；当fmean 对应的相位大于180°时，增大L 值，直至fmean 对应的相位正好为180°。

(www.xing528.com)

图7-8　耦合腔设计仿真结构

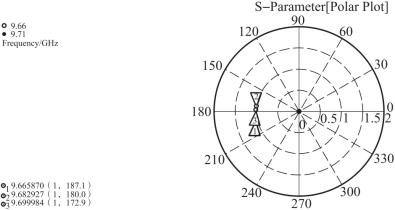
图7-9　fmean 刚好在180°的Smith 图

（3）不同结构需要移动金属棒的位置不同。经反复试验，此种加速结构将短路金属棒移动至加速腔中心位置，能使加速腔失谐。保持Lmean 不变，设定波导末端为磁边界。利用MWS 中的频域快速求解其S11 参数。如果fmean 的相位大于0°，增大b 值；反之，减小b 值，直至fmean 的相位正好为0°，此种方法相对直接利用本征模求解器求解耦合器的谐振频率更快。得到b 值后可以求解出耦合器的谐振频率，得到f= fmean。这部分是调谐过程。

（4）此时，再观察图中fπ/2、f2π/3 相应相位的角度大小。如果两者相位的差值大于120°，耦合是欠耦合，需要增大耦合口的尺寸以减小两相位之间差值；如果它们之间的相位差值小于120°，耦合是过耦合，需要减小耦合口的尺寸以增大它们之间的差值，直至两相位之间差值为120°。如以上步骤均满足设定条件，最终用理论计算得知耦合度为1。

（5）调谐和调耦合度之间是相互影响的，每一步的改变都改变前一步的结果，所以在达到加速腔失谐时fπ/2、f2π/3 对应的相位分别为60°和300°，fmean 的相位与失谐耦合腔时的fmean 的相位相差将近120°时，在不改变尺寸的情况下，需要重复（2）、（3）、（4）的步骤，直至每一步的结果都满足上述条件。调配好的Smith 图如图7-10 所示。

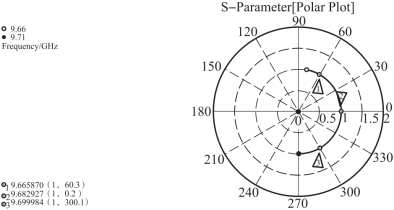
图7-1　0 调配好的Smith 图

上述步骤是在三频率法的基础上，加上笔者在调配过程中总结的经验得出的较为快速的调配方法，两种求解器可以相互佐证。

3.基于CST 软件的仿真与分析

在耦合器调配工作完成后，利用得到的匹配尺寸，在MWS 中建立一个四单元对称结构模型，因为四单元的模型在调配完好的情况下相移恰好为360°，便于以后在模拟得出的结果中用以验证调配的效果。耦合腔测试仿真模型如图7-11 所示，图7-12 所示为微波耦合电场示意图，可以看出它们具有很好的周期对称性。

图7-1　1 耦合腔测试仿真模型

图7-13 所示为四单元模型结构的S 参数曲线，可以看出频率在9 700 MHz 附近时其反射系数S11 为-54.97 dB，传输系数S12为-0.000 2 dB，则ρ=（1+S11）/（1-S11）=1.001，得出的传输效率接近100%，证明耦合器调配良好。不难看出，在9.7 GHz 附近有十几MHz 的小于-26 dB 的通带范围，说明此耦合器性能良好。

图7-1　2 微波耦合电场示意图

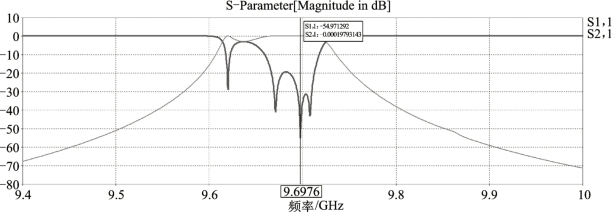
图7-1　3 四单元模型结构的S 参数曲线

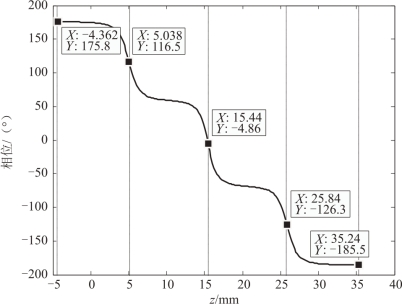
图7-1　4 四单元模型结构的相位变化示意图

图7-14 表示的是四单元模型结构的沿监视线的电场相位分布，从图中可以看出，输入输出耦合腔相移分别为59.3°、59.2°，中间两个加速腔的相移分别为121.36°、121.44°。四个腔的相移接近满足理想情况下的相移，总的相移为361.3°，与理想情况下的360°符合较好。输入耦合腔的前半部分和输出耦合腔的后半部分为驻波场，而输入和输出耦合腔靠近加速腔的部分为行波场，四个腔相当于3 个完整的2π/3 模式的行波场，总相移为360°。

图7-15 表示的是四单元模型结构沿轴线（监视线）的电场振幅分布，可看出到束流孔末端电场基本为零，可以看出，轴向电场的幅度总体是呈周期性对称分布的，加速腔中的电场幅度最大值略大于耦合腔中的电场幅度最大值，这是因为调配得到的尺寸中，加速腔的内径略大于耦合腔的内径。

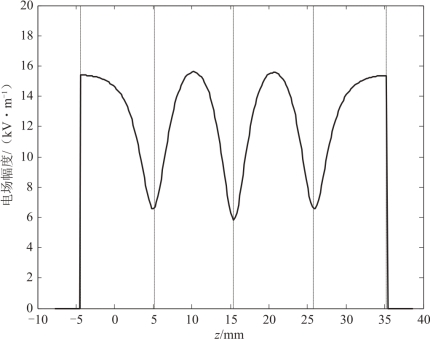
图7-1　5 四单元模型结构的电场幅度示意图

至此耦合器的设计基本完成，考虑添加束流通道或接同轴负载时将模型做适当的调整即可。基于篇幅限制，这里没有详细讨论单边耦合器的场不对称问题。事实上减少加速腔中场不对称性的方法有多种，采用偏轴单边耦合器［1］是最简单有效的方法。另外采用电耦合对称输入耦合器［1］、介质棒加载耦合器［18］等也能很好地抑制不对称场问题。