盘荷波导电磁场理论及计算

在行波直线加速器中，由于电子的速度总是小于光速，因此需要采用慢波结构使加速腔中的微波相速度降低，保持加速电子与微波场的相位同步，从而达到行波加速的目的。在行波加速器中，最简单有效的慢波结构当属盘荷结构，也叫作盘荷波导。盘荷结构作为一种慢波结构，同时也是一种周期结构。盘荷结构可以看作在圆波导中加入了周期性的带孔盘片，可以有效降低其间传输的微波相速。由于圆波导的相速总是大于光速，为了加速电子，必须降低它的相速，使之接近或小于光速，周期性的盘片将圆波导分割为很多个腔体，其中一个腔体可以看作一个周期。

1.盘荷波导慢波场

盘荷波导截面示意图（加速腔结构关于中心点对称，取中心点为图中原点）如图7-3 所示，阴影部分为盘荷结构的盘片，其他为真空区域。为方便描述，以rc 为边界线，其下的沿轴真空区域为Ⅰ区，其上的真空区域为Ⅱ区。这里只考虑角向均匀的TM 模，在圆柱坐标系中求各区域场分量的级数表达式［4］。

区域Ⅰ为近轴区域（0≤r≤rc，- D/2≤z≤D/2），为慢波区，这里的电磁场为行波场，TM01 模场分量按级数（m、n 范围为负无穷到正无穷）展开为

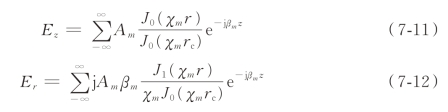
图7-3　盘荷波导截面示意图

这里的Am 为场的不定系数，β0 为基波的相位常数。

区域Ⅱ为凹槽区（rc≤r≤b，- z1≤z≤z1），可以看成在r=b 处短路的径向传输线，z 方向为驻波，其电磁场表达式为

当ξn 为虚宗量时，

这里的Bn 为场的不定系数，当n 为奇数时为jsin（ηn z），当n 为偶数时，。

2.色散方程

考虑到两个区域在r=rc 的边界上连续，则由式（7-12）和式（7-18）整理化简可得

这里的

当n 为偶数时，上式取加号，奇数时取减号。

考虑盘片倒角时，场分析法难以求解。采用变分法可转化为求解式（7-29）的非零解。

其中

要想式（7-29）有非零解，根据线性代数则有

式（7-31）即为所求的色散方程［5-8］，通过求解此方程可以得到加速腔的基本尺寸。

3.参数计算

在求得盘荷波导的基本几何尺寸后，基于式（7-29）计算其对应的A 值，可得到结构腔中的电磁场表达式，然后就可以求盘荷波导的基本物理参数，如功率流P、储能密度W、串联阻抗RS、分路阻抗RM、品质因数Q、衰减系数α 等。这些微波特性参数是衡量高频加速腔加速性能的重要指标。

1）盘片孔径功率流P

在盘荷波导中近轴处为行波，远轴处为驻波。研究行波在波导中的传输及损耗特性是十分有必要的，在盘片孔径处（图7-3 的z=D/2 处）通过横截面的功率流P 可表示为

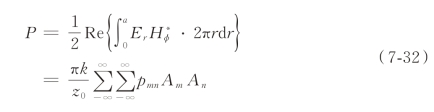
其中

2）腔内总储能密度W

为了便于计算品质因素以及群速度等参数的计算，总储能密度是一个关键量，其数学表达式为(www.xing528.com)

3）腔内壁功率损耗PL

微波在波导传输中在波导壁上损耗一部分功率，一般以热能的形式表现出来，损耗功率程度一般取决于波导材料的电导率以及微波的趋肤深度，其表达式为

式中：R= 1/（σδ）为表面电阻；σ 为金属电导率；δ 为趋肤深度。趋肤深度的一般公式为，这里的ω 为电磁场角频率，μ 为磁导率，σ 为电导率。

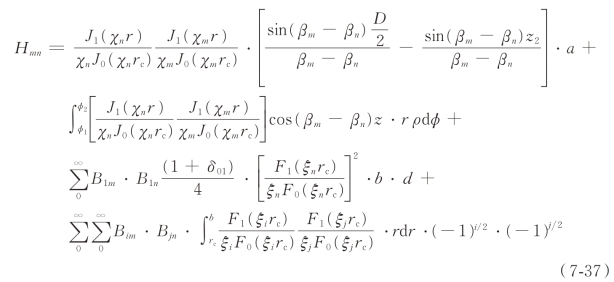
4）其他主要参数

求得P、W、PL 后，则可由式（7-38）～式（7-42）求衰减系数α、特征阻抗RM、串联阻抗RS、群速度βg 和品质因数Q：

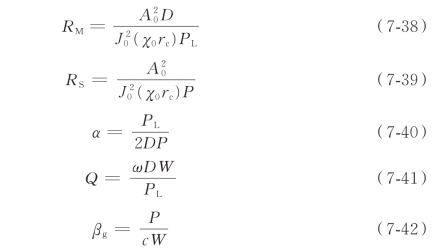
通过上述一系列公式即可计算出相关的分路阻抗、品质因数、群速度以及衰减因子等加速器设计核心参数，不难看出整个计算的核心就是求解结构中的电磁场表达式。采用变分法编程计算是求解基本尺寸和电磁场的有效方法之一，下面具体讨论其实现过程。

4.程序编制

1）程序功能讨论

在加速器设计及分析过程中，主要涉及基本尺寸求解、腔体频率求解、电磁场求解以及相关微波特性参数求解这四个方面的内容。根据上一节提到的变分法计算方法，可编制对应的程序，包括以下几个功能［5-8］。

功能A：给定设计频率f 和沿轴向的相位传播常数β0 与其他基本尺寸，计算确定盘荷波导半径b。

功能B：给定盘荷波导半径b 和沿轴向的相位传播常数β0 与其他基本尺寸，计算确定盘荷波导RF 频率f。

功能C：给定盘荷波导的微波频率f 和沿轴向的相位传播常数β0 与基本尺寸，计算确定盘荷波导的空间谐波幅度、分路阻抗、串联阻抗、群速度和品质因数。

功能D：计算边界上的电磁场和区域内任意点的电磁场。

2）多种盘片结构考虑

为了便于对照和辅助加工，提高程序的兼容性，可以在程序中考虑如图7-4所示的四种圆弧孔径结构。由于单元腔关于其中心对称，这里仍取单元腔的1/4来研究。图7-4（a）和（b）这两种结构考虑的倒角为1/4 圆，且圆弧半径小于或等于盘片厚度的一半，两者的区别在于图7-4（b）结构的δ= 0。图7-4（c）和（d）两种结构的倒角圆弧小于1/4 圆，且圆弧半径大于盘片厚度的一半。

图7-4　四种圆弧孔径结构

根据图7-4 所示，不同的盘片结构，其计算所用边角参数r 和z 值分别可表示为：

对于图7-4（a）、（b）两种结构有

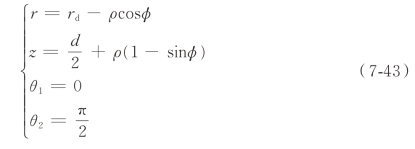
对于结构图7-4（c）有

对于结构图7-4（d）有

3）程序流程

单个程序难以同时实现前面所述的四个功能，综合考虑需要编制三个程序。其中，实现A 功能的程序1 流程示意图如图7-5 所示，实现B 功能的程序2的流程示意图与程序1 类似，只需要更改b 和f 位置，即利用参数b 为初始条件计算f。

实现功能C 和功能D 的程序3 流程示意图如图7-6 所示。

图7-5　程序1 流程示意图

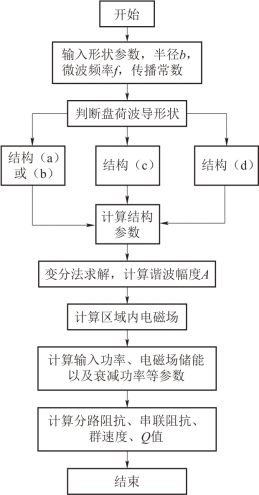
图7-6　程序3 流程示意图

基于上述程序就可以进行加速腔设计及性能分析，一般具有较好的精确度。其结果可与CST、SUPERFISH 等电磁仿真软件相互比对，辅助参数优化和腔体加工。需要指出的是，本节的电磁理论是针对TM01 模而言的，事实上，加速腔内的电磁场除了基模以外，还存在大量的高次模分量［8-9］，这些高次模分量对加速过程几乎不起作用，因此在低频段加速器中常常不做考虑。但是在高频段（C 波段以上）、大电流等情况下其高次模场强会急剧增大，对束流品质甚至稳定性造成显著的影响，此时需要重点研究并考虑抑制方法［9-11］。