粒子场互作用算法优化

由图5-3 所示的电磁PIC 方法流程可知，电磁场计算和粒子与场的互作用是电磁PIC 方法中最为基础也是最重要的两个算法，基于5.4.5 节的粒子模型与运动方程，这一节着重介绍粒子与场相互作用的过程及其算法实现。为了便于描述，这里同样以直角坐标系为例进行讨论和分析，柱坐标系和极坐标系下的情况可以类似推出。

1.场对粒子的影响

由图5-4 的Yee 网格模型可以知道，电场分量是在棱心上的，而磁场分量是在面心上的，粒子则可能存在于网格中的任一位置，所以对于粒子的运动方程式（5-53）并不能直接使用。为了完成这一目标可分为两步来实现：首先将半网格上的电磁场分量权重到整网格上，然后再插值到粒子所在的位置。

首先来讨论第一步，将半网格上的电磁场权重到整网格。可以考虑将电场平均权重到网格线两端点上，对于磁场则平均权重到网格面四个角点上。以整网格点（i，j，k） x 方向的场分量求解为例，有如下权重方法［25］：

其他方向的电磁场权重公式可类似得出。

然后是第二步，将整网格上的电磁场插值到粒子在网格中的实际位置。如图5-6 所示，假定粒子A 距离三个坐标面的距离分别为sx、sy、sz。不妨设定：

则对应的权重因子w 有如下计算式：

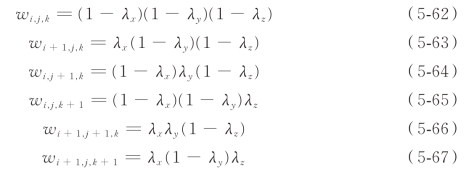
图5-6　Yee 网格中粒子位置示意图

其中，w 的下标是对应的网格索引。由此可以得出，粒子A 处x 向场分量分别为

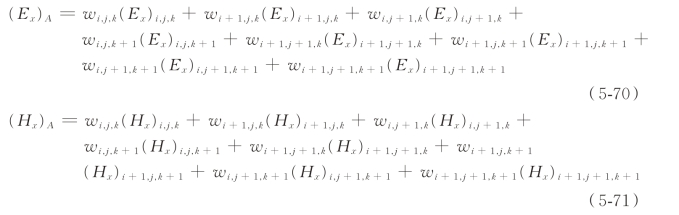
同理可以推出其他方向的场分量。

至此对应于每一个宏粒子的电磁场分量可以明确得出，再由式（5-53）和式（5-54）即可求出对应宏粒子的位移和动量变化。

2.粒子对场的影响

场对粒子的作用过程是一个推动粒子、改变其动量和位置的过程。而这一过程中空间的电荷密度和电流密度必然也会发生改变。根据Maxwell 方程组，这一改变同样会对场有着较大的影响。下面对这一影响进行详细的分析。

1）粒子推进对空间电荷密度的影响

首先考虑对空间电荷密度的影响，可以参照上一小节对场的权重，假设一个粒子被推动到图5-6 的网格内的A 处，则电荷的权重［25］可类似地表示为

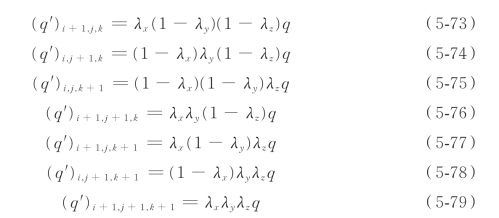(www.xing528.com)

式中：q′是该宏粒子对所在网格八个整网格点的电荷量的权重，下标为对应网格点的索引；q 为宏粒子所带的电量。

这样整网格点的电荷密度就可以重新计算得到，计算式为

式中：Q 为所有宏粒子对该整网格点的电荷量权重的总和。

2）粒子运动对空间电流密度的影响

下面来分析粒子位置的改变对空间电流密度的影响。假设粒子从n 时刻运动到n+1 时刻，从A 点到了B 点，如图5-7 所示，假定它的轨迹是平行于坐标轴的，则一共有如图5-8 所示的六条随机路径可供选择来分配空间电流密度。由于稳定性条件可知，宏粒子在每个时间步长最多只能跨越一个网格，这里就以这种情况为例进行描述。假定rx（i，j，k）、ry（i，j，k）、rz（i，j，k）分别为网格（i，j，k）的x、y、z 方向的坐标。

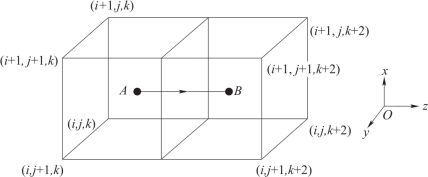
图5-7　粒子位置改变示意图

以粒子从A 点沿x 方向运动到B 点所在yz 平面为例，将运动分解为两个部分来形成电流密度。粒子沿x 方向运动产生的电流，即粒子从n 时刻起运动到yz 面网格（i + 1，j，k）处所产生的第一部分电流密度为

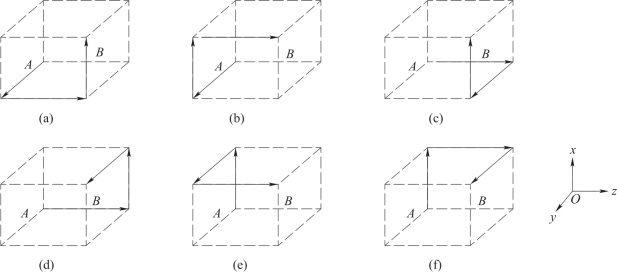
图5-8　粒子随机运动轨迹示意图

而从yz 面网格（i + 1，j，k）运动到n+1 时刻（B 点位置）所产生的第二部分电流密度为

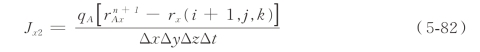
然后将电流Jx1 和Jx2 分别权重到网格上去，如图5-9 所示为网格（i+ 1，j，k）在平面yz 的投影图，投影点的位置为，sy、sz为粒子到网格面的距离。

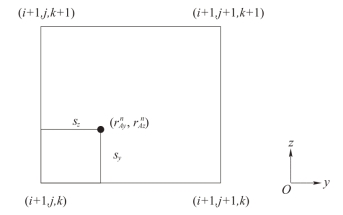
图5-9　电流密度分配YOZ 平面投影图

首先类似于前面的权重方法，可以假定：

就可以得到Jx1 分配表达式如下（Jx2 可以类似得到）：

同理可以得到粒子向其他方向运动的电流密度表达式［25］。将上述表达式代入迭代公式即可求得粒子运动对场的影响。