离散网格和时间模型的优化

电磁粒子模拟方法的时间迭代是建立在时域有限差分方法基础上的，即所谓的Yee 网格［18，24-25］单元。其基本原理是：把连续时间域内的问题转化为离散时间域的问题，即用各离散时间点上的数值解来逼近连续时间域内的真实解，是一种近似的计算方法。即使是近似方法，根据目前计算机的容量和速度，对许多问题都可以得到足够高的计算精度。

Yee 网格单元是FDTD 算法的基础。图5-4 （a）所示为直角坐标系中的Yee 网格模型，其中三个方向的电场分量和磁场分量分别用Ex、Ey、Ez 和Bx、By、Bz 表示。在Yee 元胞连续排列组成的整个空间网格中，每一个磁场分量由四个电场分量环绕；同样，每一个电场分量由四个磁场分量环绕。这种电磁场分量的空间取样方式不仅符合法拉第感应定律和安培定律的自然结构，而且这种电磁场各分量的空间相对位置也适合Maxwell 方程的差分计算，能够适当地描述电磁场的传播特性。从图中还可以看出，一般情况下，电场和磁场在不同方向上的分量位于不同方向空间全网格或半网格的位置，采用的是传统的中心差分方法，具有二阶精度。而在柱坐标中的Yee 网格模型如图5-4（b）所示，其电磁场分量的放置与直角坐标系基本类似。

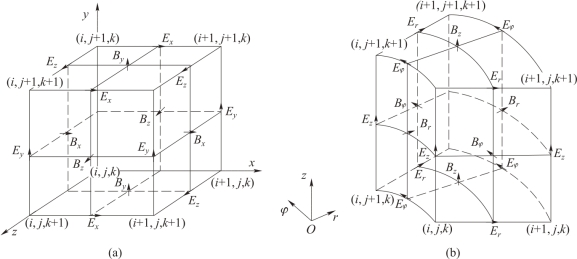
图5-4　两种坐标系下的三维Yee 网格单元(www.xing528.com)

图5-5 是电磁PIC 方法的时间离散模型（蛙跳模型）［18，23］。在场更新方面，电场E 在整数时间步长计算，而磁场B 在半时间步长计算；在粒子处理方面，粒子受力F 和位移x 的求解在整数时间步长，而粒子的动量p 求解在半时间步长。

图5-5　粒子模拟蛙跳格式示意图

从图5-5 可以看出，根据变量计算的时间点，可以划分为全时间步变量和半时间步变量，这些变量在时间顺序上交替取样和更新，取样和更新时间间隔彼此相差半个时间步，又保证了每个时间步内只取样和更新一次，能实现时间上的快速迭代求解。