空间传输的两大挑战

空间传输的两大主要难点是束流发散和地磁场影响。地磁场影响主要是影响传输定位的精度，以及限制传输的最大作用距离，对束流空间应用的功能、模式及轨道等都有着较多限制；而束流发散则是对远距离传输束流的能量、束流强度等参数有着很大的限制，是带电粒子束空间应用的基本障碍［11］。本节基于束流空间应用的目的，分别对这两大难点进行详细的讨论。

1.束流发散

带电粒子束在真空传输过程中会受到源于静电排斥的扩散。真空中的带电粒子束表面粒子受到的径向作用力可表示为

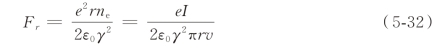
式中：ne 为束中粒子密度；r 为束半径；ε0 为真空介电常数；γ 为粒子的相对论因子；I 为束流流强；v 为粒子的运动速度。这个径向力是呈放射状向外的，其作用是将粒子推开，推开之后束半径增加而束流密度减小，此时径向受力也相应减小。不难看出：①Fr 为恒正数，这意味着真空传输的束流只可能发散，这是由其物理性质决定的；②提升相对论因子对减小扩散力十分有效，因此采用较高能量的相对论束流是必须的。对于电子束而言，MeV 量级以上，随着电子能量的提升，相对论因子迅速增加，相应的径向作用力迅速下降，对于离子束则一般要GeV 量级以上才能够达到显著的相对论效应。

束流发散程度主要与束流能量、束流强度、初始束流半径以及初始发射度等因素有关：能量越高、束流强度（或束流粒子密度）越低、束流半径越大、初始发射度越小，则其扩散程度也越小。要想减小扩散，基本上只能从提升束流能量、降低束流强度（或束流粒子密度）、提升初始束流半径以及降低初始发射度这几个方面着手。对于MeV 量级以上的粒子束，这几类提升都伴随着系统体积、重量等参数的迅速增加，在空间应用中都具有较大的限制，亟须寻找新的应用机理或模式来突破这些限制。

在空间传输过程中，在低束流密度情况下能够因为等离子体背景中和而适当改善，但其应用前景较为受限。而在高束流密度情况下基本只能依靠大幅提高粒子能量、降低束流密度来改善扩散程度。因为空间背景等离子体非常稀薄，在高束流密度情况下，背景能够中和的空间电荷基本可以忽略不计，此时可以近似看作真空传输。

2.地磁场影响

地磁场对于电子束的最主要影响是洛伦兹力偏转引起的，一方面是由于偏转引起的传输距离限制，另一方面是由于偏转的不确定性造成定位偏差。下面分别对这两种影响进行专门的探讨。

1）地磁场对最大传输距离的影响

地球轨道磁场强度随着轨道高度的增加而变小，地球表面的磁场强度典型值约为30 000 nT，在同步轨道上约为100 nT。能量电子在空间磁场环境中传输时，电子束在洛伦兹力影响下做回旋运动。电子束传输方向与磁场方向垂直时，产生的洛伦兹力最大，回旋半径最小。在一般情况下，电子束通常不会始终以垂直于磁场的方向传输，它的方向随纬度、经度和海拔高度的变化而变化。因此人们总是期望粒子束的射程范围要小于这一回旋半径，因为如果粒子束的期望射程大于回旋半径，粒子束可能会无法达到靶目标。

电子在磁场中的回旋半径可表示［11］为

(www.xing528.com)

式中：R 为电子回旋半径；γ 为相对论因子；m0 为电子静止质量；β 为电子的相对速度；c 为光速；e 为电子电量；B 为磁场强度。表5-1 给出了不同能量电子在两个不同地球轨道高度上的电子回旋半径，电子能量分别取1 MeV、10 MeV、30 MeV、100 MeV、1 000 MeV，轨道高度为1 000 km（低轨）时磁场强度的典型值为30 μT，轨道高度为36 000 km（同步轨道）时磁场强度的典型值为100 nT。

表5-1　不同能量电子在两个不同地球轨道高度上的电子回旋半径

从表5-1 可以看出，对于10 MeV 以上的电子，其回旋半径与相对论因子成近似线性的关系。在低轨道，即使采用1 GeV 的电子束，其回旋半径也仅为111 km；对于10 MeV 量级的束流则仅仅只有几km。因此可以说，电子束在低轨道的传输射程很短，低于1 GeV 以下的应用都受到极大的限制。在同步轨道，10 MeV 量级电子的回旋半径就已达到百千米量级，并随着能量提升迅速增加。因此，电子束空间传输在同步地球轨道的应用前景较好。

由上面的讨论不难得知，对于能量大于2 MeV 的相对论电子束，电子的回旋半径与其相对论因子近似成正比，与磁场强度成反比。提高电子能量，相应的相对论因子迅速提升，就可以提高电子束的传输射程。但是空间电子束系统的电子能量提高在工程上受到系统体积、重量以及能量等因素的极大限制。

2）地磁场预测精度对最大传输距离的影响

电子束传输不确定范围与空间磁场模型预测误差之间关系［11］如下：

式中：ΔR 为电子束传输距离为R 时的位置不确定值；R 为电子束的传输距离；ΔB 为磁场模型预测值与真实值的差；B 为空间磁场的真实值；定义ΔB/B 为磁场不确定度。从式（5-34）可知，电子束空间传输随着传输距离的增加，其空间位置的不确定性也越大。当磁场精度为1‰时，传输1 000 km 后，电子束斑位置不确定范围约1 km。如果此时束斑仅为10 m 量级，则空间瞄准的难度将非常大。

想要解决偏转不确定性问题，首先需要解决的是地磁场的精密测量或者建立高精度磁场预测模型。由于地磁场即使在特定轨道下也与纬度、经度、海拔高度、一天的时间、一年的季节甚至太阳黑子活动等因素都有关系，因此想得到地磁场精确模型是一个复杂的问题。经过多年的研究［12-15］，这一模型已达到一定的精度，误差可以控制在3%左右。第二种方法为地磁场精密测量，在较短距离传输时，直接测量当前的地磁场大小作为基准磁场，这一方法在较短距离（百千米以内）具有一定的可行性。

在远距离传输时，对磁场精度的要求相当高，一般要求至少1‰以上。然而建立高精度空间地磁场模型的难度很大，其精确度也难以评估。当前同步轨道的地磁场模型［15］主要以Tsyganenko 模型和MHD 模型为代表，离1‰ 以上的精度要求还有一定的距离。

空间中测量磁场的最常用仪器是磁强计［9］。磁强计的种类包括霍尔效应磁强计、核磁共振磁强计和磁通门磁强计。最常用的磁通门磁强计使用两根具有很强导磁性的杆，在没有外磁场作用时，两根杆的主线圈的感应磁场大小相等，且方向相反。在有外磁场作用时，两根杆的感应磁场大小不同，可由附加电路测量得到。磁通门磁强计的精度为0.1～2 nT，对于地球同步轨道而言，这一精度并不算太高，但最高精度已接近1‰。磁强计只能测量平台附近的磁场大小，对于传输路径上各点的磁场则难以测量，对于远距离传输时精度会大幅下降。可以考虑将磁强计与预测模型综合使用，有可能进一步提升预测的精度。

无论采用上述哪种方法，粒子束传输都需要经历以下几个过程：估算传输路径、发射粒子束、跟踪束轨迹、重新估算传输路径并调整发射参数、发射粒子束。这几个过程多次反复才有可能将粒子束投射到靶目标上。这就属于定位方法的研究，解决方法及技术途径可以参考和借鉴传统的激光束定位与控制技术。