地球磁场的建模方法，地磁场模型的建立和评价是一个复杂的过程

地磁场模型的建立和评价是一个复杂的过程，不仅涉及模型计算方法，而且涉及模型计算时的定解条件和计算技巧的选取，更涉及测点的布局和观测数据的处理过程等［26-27］。建立地磁场模型的方法有多种，如球谐分析［28］、球冠谐分析［29］ 和矩谐分析［30］ 等。此类方法基于高斯磁位理论，在确定的定解区域和定解条件下展开并建立地磁场3 个独立分量的统一模型。由于此类方法所获得的模型物理意义明确，研究者可以借该类模型对地磁场的三维结构及其变化过程进行理论分析与探讨；又如，多项式拟合［31-32］等，此类方法分别对地磁场的独立分量在某一空间区域内的分布进行拟合。由于计算过程相对简便，因此在实际使用中，如制作嵌入式导航定位系统时此类模型有着广泛的应用。

1.经典球谐模型

当前世界上绝大多数的地磁场模型都是基于高斯提出的球谐分析模型［26］而建立的。当一个区域内部既无磁性物质，又无电流流动时，磁场有标量位存在，它满足拉普拉斯方程。在球坐标系中，拉普拉斯方程的解可以写成球谐级数（Series of Spherical Harmonic Functions）的形式。建立主磁场模型所依据的地磁测量大多是在地面和近地表的底层大气中进行的，不妨合理地假定，这一空间范围的大气是无磁性和绝缘的。卫星磁测虽然在高空进行，但是电离层和磁层电流体系对所测磁场的贡献可以借助已有的模型消除掉，从而得到标量位场部分。这样，可以在球极坐标系中写出主磁场标量位U（r，θ，λ，t）所满足的拉普拉斯方程［26，33］

式中：r 是地心距；θ 是地理余纬度；θ= 90° - φ，φ 是地理纬度；λ 是地理经度；t 是时间。主磁场的磁感应矢量B（r，θ，λ，t）可以表示成标量磁位的负导数B= -∇U，主磁场是起源于地球内部的，它的拉普拉斯方程解可以用分离变量法求出，并写成球谐函数的形式

相应的内源磁场分量为

在上述表达式中，上标i 表示内源场。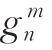和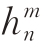叫高斯系数或球谐系数，如果n 的最大值取为N，则称N 阶截断，此时系数 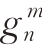有N（N + 3）/2 个，系数有N（N + 1）/2 个，所以，球谐系数共有N（N + 2）个。

上面讨论了拉普拉斯方程解的一部分，即包含（ar ）n+1 因子的部分，它表示磁场源在地球内部，叫作内源场。而拉普拉斯方程的完全解由两部分组成，另一部分包含（ra ）n 因子，表示磁场源在地球外部，即外源场。借助地表的地磁观测，可以将这两部分磁场分别求出来，这是高斯理论最重要的结论之一。

包含内源场（用上标i 表示）和外源场（用上标e 表示）的总磁位可以写成

相应的内源场分量由式（4-9）表示，外源场分量为

国际地磁学和高空物理学协会（International Association of Geomagnetism and Aeronomy，IAGA）定期发布国际地磁参考场（International Geomagnetic Reference Field，IGRF）模型，这些模型只包括内源场。这是目前世界上应用最为广泛的全球地磁场模型。每5 年，IAGA 都会发布一个新的IGRF 模型，球谐系数随时间会发生变化，新的模型会修正上一个模型的地磁场模型系数，并提供最新的地磁场模型和未来5 年内的长期变化模型。地磁场模型的阶数为13，长期变化模型的阶数为8。目前最新的IGRF 模型是2015 年发布的IGRF-12［34］，IGRF-12 一共拥有1900—2015 年的24 个主磁场模型和2015—2020 年的长期变化模型。(www.xing528.com)

对不同区域和不同的使用场合，要求对主磁场做不同近似程度的描述，这相当于在球谐级数中取不同的截断水平，于是产生了许多地磁场模型，如使用于近地区域的地心共轴偶极子模型（Geocentric Coaxial Dipole）、地心倾斜偶极子模型（Geocentric Inclined Dipole）、偏心偶极子模型等，为了描述磁层磁场，产生了适用于磁层的Mead-Williams、Cheo-Beard、Tsykanenk ［35-37］ 等模型。与不同地磁模型相对应，定义了不同的坐标系，如地心偶极坐标系、偏心偶极坐标系、倾角坐标系、B-L 坐标系以及各种磁层坐标系。这些模型和坐标系都可以看作是高斯球谐模型的简化或变化而来。

基于多年的研究，除了IGRF 模型外，高精度的全球模型还有CHAOS 模型［38］、CO2 模型［39-40］、CM 模型［41］等。这些模型的基础都是球谐理论，在高精度的磁测数据和改进的建模方法下，具有更高的截断阶数和精度。同时这些模型也改进了对外源场的计算方法，使外源场的计算更加准确。例如，CO2模型在计算外源场时增加考虑了磁层环电流的因素，在模型中增加了Dst（Disturbance storm time，扰动暴实时）指数。CHAOS 模型中增加了欧拉角来校正由磁通计测量的矢量数据。CM 系列模型则是目前能够最彻底地分离计算地磁场各个部分的模型。

2.偶极场模型

地核主磁场占地磁场的95% 以上，并且表现为偶极子场，因此在一般精度的情况下，特别是在低轨道高度（200～400 km）及以下、中低纬度情况，都可以采用偶极子模型近似表达地磁场（或地磁场一部分），由于这一模型的简单易用，在很多情况下用于估算空间地磁场大小，这里对其进行简要的讨论。地磁场模型可以用三种精确度递增的偶极场模型来模拟：①地心同轴偶极子：偶极子轴与天体的旋转轴平行，且穿过天体质心；②倾斜偶极子：偶极子轴相对于天体的旋转轴有一定的倾斜，且穿过天体质心；③偏心倾斜偶极子：偶极子轴相对于天体的旋转轴有一定的倾斜，且不穿过天体质心，与质心有偏离。可以用球面坐标和笛卡儿坐标表示这三种偶极场模型：

其中

式中：B0 为赤道的地磁通量密度大小，T；m 为天体的磁偶极矩，A·m2；r 为半径，m；R 为天体参考半径，m；x、y、z 为笛卡儿坐标系中的位置，m；θ 为经度，格林威治以东为正；φ 为余纬。

对于模型①使用地理坐标值，而对于模型②和③采用地磁坐标值。由式（4-12）和式（4-13）可得出磁通量密度大小为

由式（4-16）可以推导出麦克伊尔文B-L 坐标系描述的偶极场公式［1］：

这一坐标系被广泛应用于描述被俘获粒子的漂移等。由于偶极场是轴对称的，B-L 坐标系可以将三维的空间坐标系转化为二维的空间坐标系。转化过程是将球坐标中的r、θ、φ 坐标转化成L、B 坐标，其中L 表示磁力线与位于地磁赤道上的地磁轴之间的径向距离，以参考半径为单位；B 表示磁通量密度的大小。由国际地磁参考场2005 的地磁场模型可知，倾斜偶极子的参数为B0 =30 036.7 nT，φg北极= 10.26°，θg北极= -71.78°，其中，φg北极和θg北极代表偶极子轴相对于地球坐标的地磁纬度和地磁经度。