如图5.4所示，机床坐标系定为OM-XYZ，A轴坐标系定为OA-XAYAZA，C轴坐标系定为OC-XCYCZC。S（XC，YC，ZC）和T（XT，YT，ZT）分别为球杆仪两端圆球在机床坐标系中的坐标。OM-OA为A轴坐标系到机床坐标系的变换矩阵，OA-OC为C轴坐标系到A轴坐标系的变换矩阵。
图5.4 各坐标系定义
机床在运动过程中的实际误差可由球杆仪两端圆球球心间距离的变化在球杆仪敏感方向上的变动得到。根据坐标变换及误差传递原理，机床在运动过程中的实际误差还可通过计算两端圆球球心在机床坐标系下的坐标变化得到。先建立各部件的坐标系，通过坐标系间的变换关系将工作台坐标系圆球球心位置变换到机床坐标系，然后计算主轴端圆球球心在机床坐标系中的位置，通过建立相关方程组即可求得参与运动机床旋转轴的误差参数。
与主轴端相连的圆球的球心随着机床与A轴在YZ平面插补走圆，主轴端圆球沿与A轴平行的轴线旋转ϕ角，则坐标在机床坐标系下的变换矩阵可表示为TR。
主轴端圆球在运动过程中的坐标在机床坐标系下可表示为
其中，（XSXYZ，YSXYZ，ZSXYZ）为主轴端圆球的初始位置。
与主轴端相连的圆球，随着A轴的运动在YZ平面插补走圆，则与主轴端相连的圆球的运动在A轴坐标系下的变换矩阵可表示为TCA。
若A轴和C轴之间存在绕Y轴的转角误差βCA，则A轴与C轴间的旋转变换矩阵可表示为EβCA。
A轴和C轴之间的线性误差为δy CA（图5.2），工作台上圆球的球心坐标在A轴坐标系中的坐标可用TA表示。运动之前圆球球心的坐标在C轴坐标系中的初始坐标可表示为TC，则TA与TC之间的关系为
(www.xing528.com)
A轴坐标系和机床坐标系之间的转角误差βAY和γAY可表示为
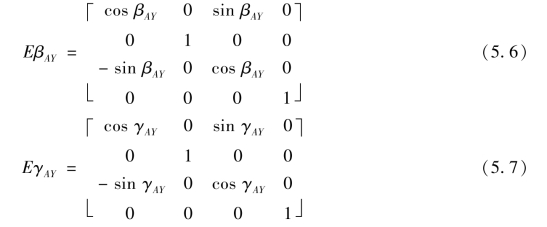
δx AY、δy AY和δz AY为A轴相对于机床在X、Y和Z方向上的平移运动误差；若A轴存在αAY转角误差，则A轴绕与X轴平行的轴转动ϕ在A轴坐标系中的变换矩阵可表示为TAXYZ。
工作台上圆球的球心在C轴坐标系中的坐标可用T来表示。
将式（5.5）代入式（5.9）可得
由式（5.10）计算可得各坐标分量分别为
根据所编制的数控程序，球杆仪以安装在工作台端圆球的球心为圆弧插补的运动中心，使主轴端圆球的球心做圆弧插补运动。由于各种误差的存在，圆球在机床上的实际位置偏离理论的位置，在机床坐标系中，假设工作台端圆球的球心的实际坐标为T（X0，Y0，Z0），主轴端圆球的球心的实际坐标为S（X1，Y1，Z1），球杆仪的实际杆长为R+ΔR。如图5.5所示，根据勾股定理可知
式（5.12）中，R的值是球杆仪的给定杆长，ΔR可以由球杆仪运行的结果得到，（X0，Y0，Z0）和（X1，Y1，Z1）的值可以由所建模的误差模型式（5.11）计算得到。
图5.5 球杆仪测量中的坐标系与误差矢量
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
