根据多体系统误差分析理论,需对多体系统在理想状态下和实际状态下的位置和姿态的变化情况分别进行分析,多体系统中各典型体之间存在相对静止和相对运动这两种状态,需分别分析多体系统的理想运动变换矩阵和实际运动变换矩阵。
(1)典型体的几何表示
于参考体B0和各典型体Bi,Bj,…,Bn分别建立静态坐标系和动态坐标系,如图2.5所示,坐标系O0-X0Y0Z0为广义坐标系,Oi-XiYiZi和Oj-XjYjZj分别为典型体Bi和Bj的动态坐标系,点Oi到点Oj的位置变化表示两个典型体间的运动变化情况,其中,矩阵Tijp为理想的静止位置矩阵,矩阵Tijs为理想的运动位置矩阵,Tijp和Tijs分别用4×4的齐次矩阵表示。
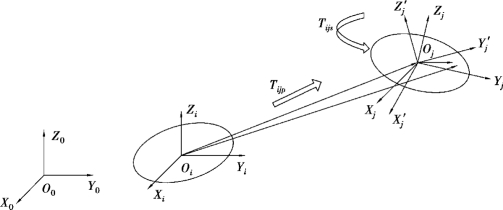
图2.5 理想状态下典型体Bi和Bj的坐标变换
(2)理想运动变换矩阵
多体系统中典型体之间的运动变换主要有坐标点的变换、平移运动变换和旋转运动变换。根据图像处理中的坐标变换方法,若坐标系Oj-XjYjZj由Oi-XiYiZi首先做旋转运动,即绕X轴旋转α,再绕新的Y轴旋转β,再绕新的Z轴旋转γ,然后做平移运动,即沿新的X轴平移x,再沿新的Y轴平移y,再沿新的Z轴平移z,则坐标系由Oj-XjYjZj至Oi-XiYiZi的理想静止变换矩阵为(https://www.xing528.com)
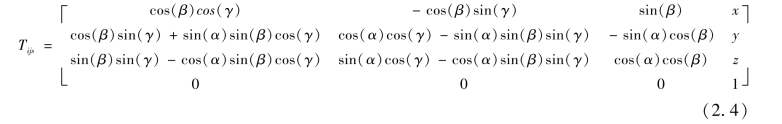
(3)实际运动变换矩阵
机床在运动过程中,由于各部件之间不仅存在静止位姿误差还存在运动位姿误差,因此,实际运动变换矩阵包括理想运动特征矩阵和运动角误差特征矩阵。若坐标系Oj-XjYjZj由Oi-XiYiZi首先做旋转运动,即绕X轴旋转α的误差角为Δα,再绕新的Y轴旋转β的误差角为Δβ,再绕新的Z轴旋转γ的误差角为Δγ,然后做平移运动,即沿新的X轴平移x的平移误差为Δx,再沿新的Y轴平移y的平移误差为Δy,再沿新的Z轴平移z的平移误差为Δz,则坐标系由Oj-XjYjZj至Oi-XiYiZi的实际运动误差变换矩阵为
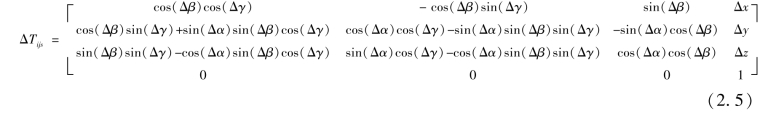
在矩阵中,当误差角Δα、Δβ、Δγ很小时,可以忽略高阶“无穷小”,ΔTijs可以变为
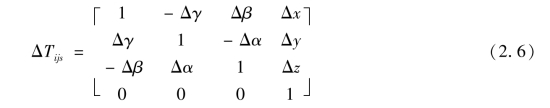
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




