CORDIC-DDC结构在信号处理中的应用

从图4－18可知，正交DDC变换输出的I、Q分量分别为I（k）=sIF（k）cos2πfNCO k，Q（k）=sIF（k）sin2πfNCO k，如果写成下列向量形式：

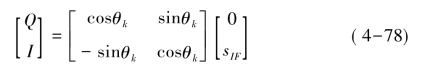
对比式（4－69）和式（4－70），我们可以推导出CORDIC－DDC结构，如图4－23所示。

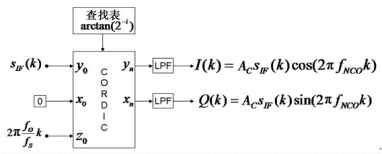
图4－23　CORDIC－DDC结构示意图

当y0为中频采样信号sIF，x0为0，z0为数字本振的瞬时相角θk，则经过CORDIC－DDC运算，可以得到所需的正交I、Q分量。图4－23中的为CORDIC－DDC算法的补偿因子，可以当作后级滤波器的处理增益而不做校正，或者在滤波器设计时引入校正因子进行补偿。(www.xing528.com)

分析式（4－75），可知操作的最大旋转角度Z max为：

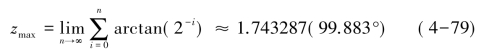
为了将DDC的计算角度从－99．883°～99．883°扩展到－π～π，根据实际DDC角度需要，可以在CORDIC－DDC之前预先进行90°旋转（当θ为正时顺时针旋转，否则逆时针旋转）。即

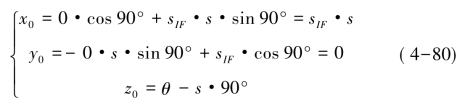
因此，CORDIC－DDC变为（N+1）次旋转迭代。为了使DDC速度与中频采样输入信号速率匹配，采用如图4－22（b）所示的全流水线结构高速完成CORDIC－DDC算法。

可见只需要移位、加法操作，以及一个小的acrtan值的存储器，就可以实现数字下变频。不仅省去了乘法操作，还避免了节省ROM而造成的相位截断效应。CORDIC实现简单，计算速度快，很适合使用FPGA的LUT单元实现。在我们的UOSDR接收机系统中就是使用了这种CORDIC－DDC结构，并且获得了很好的效果。