理解CORDIC算法的原理

CORDIC算法最早是1959年Volder为B－58轰炸机数字导航系统中三角坐标关系运算而提出来的革命性算法。算法的基本思想是通过移位和加减迭代运算，替代矢量的旋转和定向计算中所需要的三角函数（cos x，sin x）、乘/除法、开方反三角arctanθ、指数eθ等函数，能完成多种超越函数的计算，所以特别适合在FPGA上实现。

图4－20　CORDIC坐标旋转

使一个二维平面上的矢量旋转一个特定角度，如图4－20所示，相当于将该矢量左乘一个Givens矩阵。

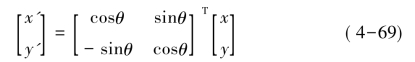
这里，［x'y'］T是［xy］T旋转θ角度后得到的矢量，式（4－69）可以改写成：

如果将θ分解为，其中θi=arctan（2－i），则旋转公式可分解成：

其中，

式（4－71）将一次特定角度的旋转分解为基于2的乘加计算，对于定点数而言，只需要进行移位加权运算。理论上，一个任意角度需要无限次旋转，但在实际中，旋转次数与输入数据的字长有关。而CORDIC运算有限字长效应的定量分析，即

式（4－73）中，Rn和R分别为有限次迭代输出值与期望输出值，δn和θn分别是有限次迭代逼近和角度量化带来的误差，fn是舍入误差。

式（4－71）中的ρi用于控制旋转方向，不同模式有不同的判断条件。用于角度旋转的CORDIC模式称为圆周模式，有两种工作方式。

（1）旋转方式(www.xing528.com)

将输入矢量旋转一定的角度，设输入矢量为［x，y］T，旋转角度为z，需要计算：

则初始化z为所需的角度，每一步的迭代计算流程为：

（2）向量化方式

根据输入矢量，得到输出y矢量为0的旋转。设输入矢量为［x，y］T，旋转角度为z，需要计算：

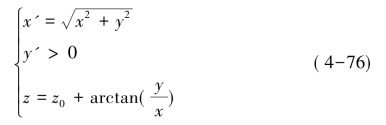
如果初始化z0=0，则最后可以得到，每一步计算流程为：

从上述的计算流程可以看出，CORDIC运算可以由一系列如图4－21所示的运算单元级联构成。

图4－21　CORDIC基本运算单元

可以使用不同的方式用如图4－21所示的运算器完成CORDIC计算，典型的方法是使用控制状态机循环迭代处理〔图4－22（a）〕，和全流水线处理〔图4－22（b）〕，或者使用状态机和流水线结合的方式。

图4－22没有给出校正的实现，通常使用一个乘法器进行幅度校正，也可以使用类似CORDIC的移位相加方式实现校正。

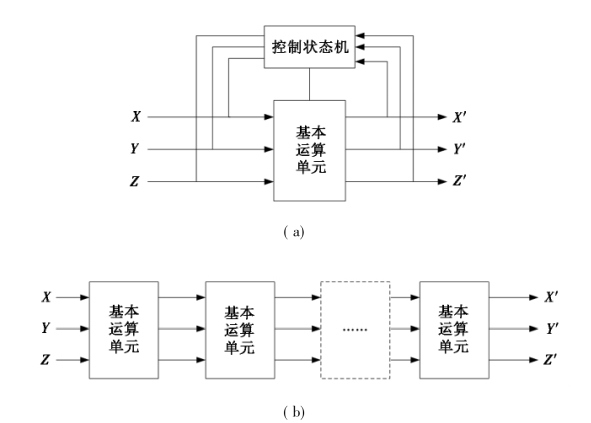
图4－22　CORDIC的构造方式