优化积分梳状滤波器(CIC)的效果

4．4．2．1　CIC滤波器原理

当抽取因子不是2M时，就不能用半带抽取，此时就需要用CIC滤波器。它不需要进行一般FIR滤波器所需要的乘法运算，只用加法运算，故具有较高的运算效率，多用于下变频第一级抽取滤波，其冲激响应具有如下形式：

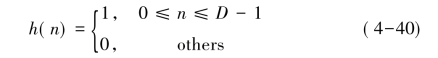
式中，D为CIC滤波器的阶数。其Z变换形式为：

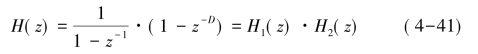
式中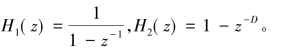

H1（z）为积分器，H2（z）为梳状滤波器（因为其幅频特性的形状如同一把梳子），CIC滤波器由这两部分级联组成，其总频率响应为：

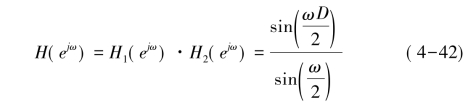
其幅频特性如图4－15所示。图中（0，2π/D）的区间为CIC的主瓣，其他区间为旁瓣。由幅频响应曲线可见，随着频率的增大，旁瓣电平不断减少，其中第一旁瓣的最高电平为：

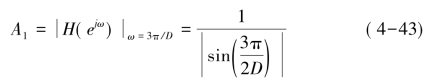
当D≫1时，

与主瓣电平D的差值为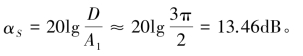

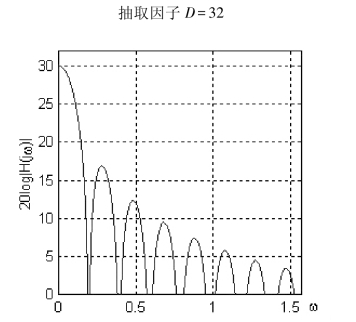
图4－15　单级CIC滤波器幅频响应

可见单级CIC滤波器的旁瓣电平比较大，只比主瓣低13．46dB，这么低的阻带衰减难以满足实际的要求。为了降低旁瓣电平，一般采用多级CIC滤波器级联的办法解决。Q级CIC滤波器级联的频率特性为：

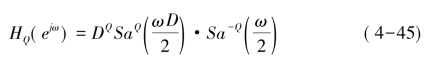
可得到13．46×Q（dB）的阻带衰减。但是多级CIC滤波器级联带来的一个问题是处理增益太高，如Q级级联，在频率响应表达式中有DQ个处理增益，随着级数的增加及抽取倍数的提高，处理增益会使系统产生溢出错误，因此在CIC前一般要用幅度衰减器。如HSP50216中，在CIC之前就使用了32bit的桶形移位器设置幅度衰减量，衰减量可以在2－45～2－14范围内设定，用户必须根据D的大小，相应地改变桶形移位器衰减的大小。同时抽取因子D的选取还需要考虑以下两个方面因素：

（1）满足阻带衰减要求。Q级CIC滤波器的阻带衰减为：

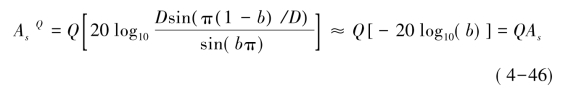
其中b为带宽比例因子，实际上是信号带宽B与抽取后的输出采样率fs/D的比值，即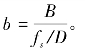当b≪1且D≫1时，上式约等号成立。显然减小抽取因子或增加输入采样率，可以获得更大的阻带衰减。(www.xing528.com)

（2）满足通带容差的要求。当D/b≫1时，Q级CIC滤波器的带内容差为：

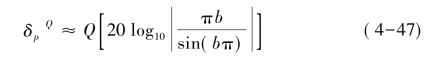
显然降低带宽比例因子，可以减小滤波器的带内容差。

可见，CIC滤波器的阻带衰减和带内容差都只与带宽比例因子有关，或者说只与相对信号带宽有关。在信号带宽一定的情况下，应尽量采用小的抽取因子或增大输入采样率，以减小带宽比例因子。也就是说，CIC滤波器一般要用在抽取系统的第一级（输入采样率最高）或内插系统的最后一级。

使用MATLAB©的mfilt．cicdecim函数可以很容易地设计和分析CIC抽取滤波器。图4－16显示了该函数设计的一个D=10，Q=5的CIC滤波器所具有的幅相特性，该滤波器的直流增益为100dB，图中的箭头表示混叠情况。对通带影响最大的是1倍频附近的信号，其功率水平与信号带宽和CIC滤波器阶数Q有关。一般通过增大阶数来抑制混叠信号的功率水平。

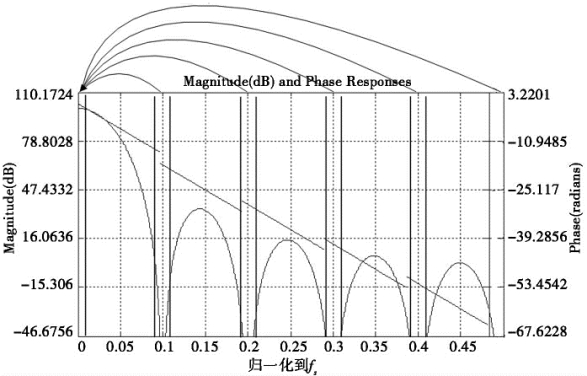
图4－16　5级CIC滤波器的幅度和相位谱

4．4．2．2　 CIC滤波器的字长设计

如图4－17所示，单级积分器在单位圆z=1处存在一个极点，这意味着积分器频率响应在直流处含有冲击，在使用有限字长的数字信号处理中，使用单个积分器就已经会造成计算结果溢出。

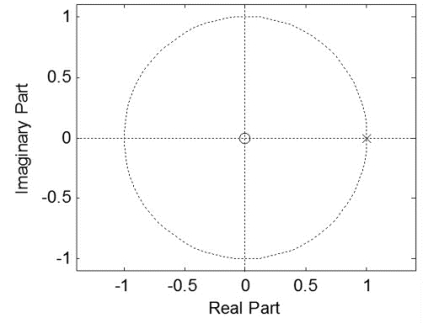
图4－17　积分器的极、零点图

但若使用二进制补码进行定点运算，设寄存器字长为L，抽取率为R，梳状滤波器阶数为M，如果单个积分器的输出动态范围能容纳梳状滤波器两个减操作数的差值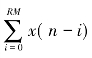，当发生溢出时，积分器输出为：

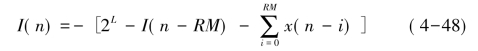
那么单个梳状滤波器输出为：

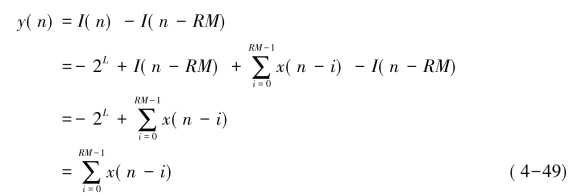
可见，只要积分器的输出动态范围能容纳梳状滤波器两个减操作数的最大差值，就不会造成滤波结果的溢出。当x（n）为单位阶越输入时，这个差值为RM，即单级CIC滤波器的直流增益。

根据式（4－48）和式（4－49），当M、n和R增长时，动态范围需要根据直流增益扩展，寄存器位宽增加

出于数据传送速率和存储器容量的考虑，必须对输出进行截断处理，Hogenauer的论文对此做了分析，通过设计可以保证级间截断噪声的累计效果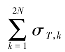不超过直接对输出截断引入的噪声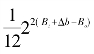，并推导出滤波器每级寄存器可以丢弃的最低有效位为：

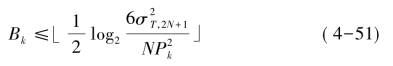
其中为k级寄存器后的方差增益。根据这个公式，我们可以计算每级寄存器字长的程序。