基于多相滤波的数字正交变换优化方案

基于直接中频采样技术的全数字化正交解调方法近年来得到了广泛的研究和应用。首先对模拟中频信号进行数字化，得到数字序列，然后与两个正交本振序列相乘，经数字域低通滤波器后获得两路正交的基带输出分量，处理过程如图4－12所示。

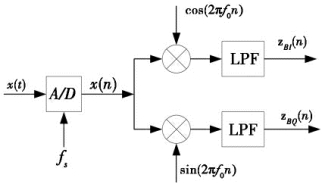
图4－12　直接中频采样及数字相干检波

在数字域进行正交变换，两个本振序列的相位正交性只受数字域表示数据的字长限制，精度非常高，正交性完全可得到保证。混频过程实际就是输入数据与本振的相乘运算。模拟域实现正交变换产生的两路基带分量相位不平衡的现象，在数字域中基本不存在。因此，数字域混频正交变换方法的应用越来越广。

该方法的主要缺点是：要在较高的频率（f0）上对输入信号数字化，对A/D采样速率的要求比较高。另外，当采样速率很高时，特别是对阻带衰减要求比较高时，会导致设计的低通滤波器的阶数太高，难以实现。解决的办法是采用基于多相滤波结构的数字正交变换方法，它不需要正交本振，而且低通滤波器的阶数也比较低。多相滤波结构的处理过程如下：

对于输入信号x（t）=a（t）cos［2πf0 t+φ（t）］，用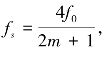m=0，1，2，…对其采样，得到的采样序列为：

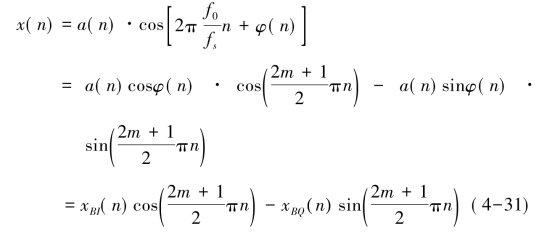
由式（4－31）可得：

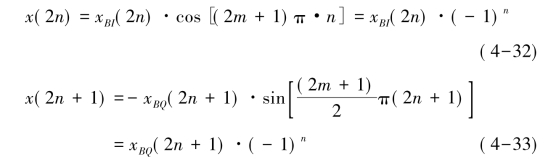
可见，同相序列的形成是先经2倍抽取，然后与（－1）n序列相乘，再经滤波后得到。正交序列的形成是先经过一阶延迟，再进行2倍抽取，并与（－1）n序列相乘后送入低通滤波器，令：(www.xing528.com)

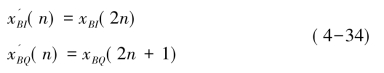
则其数字谱为：

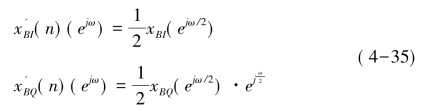
式（4－35）表示同相通路与正交通路中的低通滤波器之间相差一个延时因子ejω/2，在时域中相当于相差半个采样点，该差值是由于采用了奇偶抽取而引起的，这种时间上的对不齐可采用两个时延滤波器加以校正，这两个滤波器的频率响应要满足：

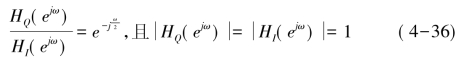
例如可选择

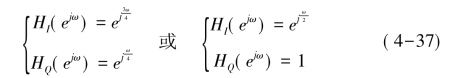
采用任一对滤波器对x' BI（n）和x' BQ（n）进行滤波，两路基带信号输出在时间上即可完全对齐。正交基带变换的多相滤波器实现原理如图4－13所示。

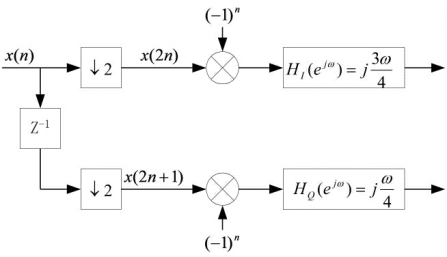
图4－13　正交基带变换的多相滤波实现