【摘要】:4.3.1.2实窄带信号的等效低通复包络正交表示我们知道一个复信号z可以用极坐标形式表示:式中a、θ分别表示z的瞬时包络和瞬时相位。将式与e-jω0 t相乘后变成零载频,便可得到基带信号:式中ZBI=acos[φ]和ZBQ=asin[φ]分别称为基带信号的同相分量和正交分量。如图4-11所示为模拟域方法实现的信号正交相干检波。图4-11模拟域实相干检波
4.3.1.1 实信号的复解析正交表示
对于一个窄带实信号x(t),若只取其正的频率分量,则所对应的复解析信号为:
![]()
其中,把z(t)称为实信号x(t)的复解析表示,把z(t)的实部称为x(t)的同相分量,虚部称为x(t)的正交分量,且这两个分量互为Hilbert正交变换,即
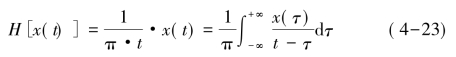
实信号的复解析正交表示具有以下作用:从时域可获得实信号的相位正交分量;从频域可去掉实信号的负频率正交分量;可通过频谱搬移得到带通实信号的等效低通复包络表示,将调制解调的表示与实现从中频(射频)转化到基带。
4.3.1.2 实窄带信号的等效低通复包络正交表示
我们知道一个复信号z(t)可以用极坐标形式表示:
![]()
式中a(t)、θ(t)分别表示z(t)的瞬时包络和瞬时相位。
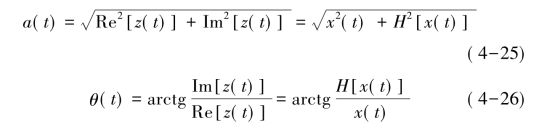
瞬时角频率![]() (https://www.xing528.com)
(https://www.xing528.com)
一个实际信号一般满足:

此时该信号被认为是窄带信号,可表示为:
![]()
其解析表示式为:
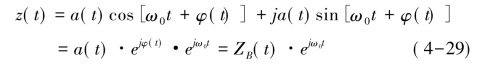
式中a(t)表示瞬时包络,ω0 t+φ(t)为瞬时相位,ω0+φ'(t)为瞬时角频率。
将式(4-29)与e-jω0 t相乘后变成零载频,便可得到基带信号:
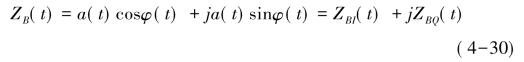
式中ZBI(t)=a(t)cos[φ(t)]和ZBQ(t)=a(t)sin[φ(t)]分别称为基带信号的同相分量和正交分量。如图4-11所示为模拟域方法实现的信号正交相干检波。
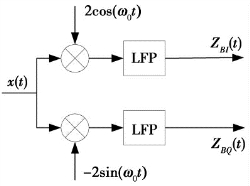
图4-11 模拟域实相干检波
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




