多级实现抽取策略

前面在讨论采样率变换（抽取、内插）时，都是按单级来考虑的，即D倍内插或抽取均一次完成。但在实际设计中，当抽取倍数D很大时，要求抽取器前的抗混叠低通滤波器的带宽很窄，所需的滤波器之阶数非常高，以至无法实现。因此，可以考虑采用分级抽取，使滤波器的阶数大为减小，大大降低对滤波器的设计要求，如图4－6所示。

图4－6　抽取的多级实现

例如，设输入采样速率为fs=40MHz，抽取倍数D=2500，即最终需要得到16kHz的采样速率，信号带宽为5kHz，5～8kHz为频率过渡带，要求通带纹波δp为0．002，阻带衰减δs小于0．001，当采用凯撒公式设计这样的FIR滤波器时所需要的滤波器阶数为：(www.xing528.com)

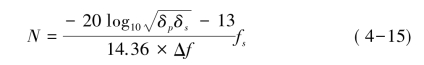
式中，Δf为过渡带宽度，fs为采样速率。

将Δf=8－5=3kHz和其他参数代入式中可得N≈40174，即要实现这样的窄带滤波器用窗函数法需要40174阶，这样高阶的滤波器是无法实现的。解决这一问题的方法就是采用多级实现。这里假设采用三级抽取，抽取倍数分别为D1=50，D2=10，D3=5，这时对第一级，要求δp1=δp/3=0．0006，δs1=0．001，Δf1=395kHz，fs1=40MHz，由式（4－15）可算出该滤波器的阶数为N1=348。对于第二级，要求δp2=δp1=0．0006，Δf2=35kHz，fs2=800kHz，由式可算出该滤波器的阶数为N2=79。对于第三级，要求δp2=δp1=0．0006，Δf2=15kHz，fs2=80kHz，由式（4－15）可算出该滤波器的阶数为N3=19。可见分级抽取后，滤波器的阶数大为减小。采用多级抽取时，对每一级滤波器设计时必须注意以下三点：一是每级滤波器的通带宽度不能小于信号带宽。二是过渡带是变化的，它取决于每一级的抽取倍数，即过渡带的截止频率不能大于该级输出速率的一半。三是对通带带内纹波的要求，假设要求带内纹波为δ，若用M级实现，则每一级的带内纹波为δm=δ/M。