整数倍抽取方法优化指南

使样本序列数据率降低的变换称为数据率抽取，也称为数据率压缩。对原始采样序列x（n）每隔（D－1）个（这里D为整数）取一个，以形成一个新序列xD（m）的过程称为整数倍抽取，即

式中D为正整数，称为抽取因子。抽取后数据速率只有原来的D分之一，大大降低了对后续处理速度的要求。对抽取后的序列进行离散傅立叶变换得：

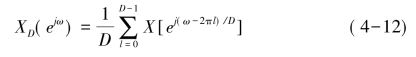
可以看出，抽取序列的频谱是原始序列频谱经D倍展宽和频移后的D个频谱的叠加和。

如果x（n）序列的采样率为fs，则其无模糊带宽为fs/2。当以D倍抽取率对它进行抽取后得到的xD（m）的采样率为fs/D，其无模糊带宽为fs/（2D）。如果x（n）中含有大于fs/（2D）的频率分量，则xD（m）就会产生频谱混叠，导致从新序列中无法恢复原始信号。因此为了保证抽取后的信号不产生频谱混叠，在抽取之前需要加一个带宽为fs/（2D）的抗混叠低通滤波器。如图4－3所示为抽取后（D=2）的有混叠的频率结构，而图4－4表示抽取后（D=2）的没有混叠的频率结构。(https://www.xing528.com)

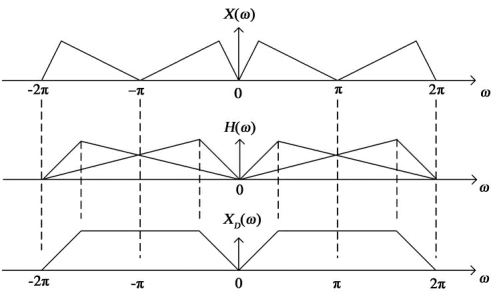
图4－3　抽取前后（D=2）的频率结构（混叠）

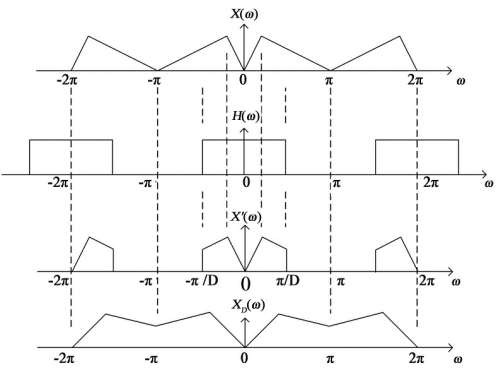
图4－4　抽取前后（D=2）的频率结构（无混叠）

这时对XD（ejω）进行处理等同于对X（ejω）的处理，但前者的数据流速率只有后者的D分之一，大大降低了对后续处理速度的要求。实际应用时，D一般比较大，这就要求抽取器前的抗混叠低通滤波器的带宽非常窄，过渡带非常陡，要实现这样的数字滤波器几乎是不可能的，因为滤波器系数将会达到几百甚至上千阶，由此引起的滤波器延迟将会很大，并且系统的特性将会不稳定。在实际设计中，当D很大时，一般都采用多级抽取，逐步降低采样率。多级抽取不但降低了对每一级抗混叠滤波器的要求，而且随着滤波器阶数的减少，所需的运算量也会大大地降低。抽取器不仅降低了输出信号的频率，而且还提高了频域分辨率。抽取器实际起到了下变频的作用，输出信号的频率降低了，但频谱结构并没有变化。

如果抽取倍数不是整数，则要用到内插技术。比如，要进行D/I倍抽取，则可先进行I倍内插后，再完成D倍抽取。