正交采样：解决混叠的过采样方式

正交采样是过采样的一种，根据Nyquist采样定理可知，若要用一组采样值恢复原来的信号，至少要采用Nyquist速率才不会产生混叠。但在实际应用中由于受到硬件性能极限的限制，在中频或射频上实现数字信号处理相对比较困难。同时从理论上考虑，载频本身并无目标信息，目标信息蕴含于载频上的调制信号之中，因此在将回波信号数字化之前，可先进行变频，将回波信号变为基带信号。

由于接收机的输入回波信号总是实信号，而实际应用中，一般总希望能同时获取回波信号的幅度信息和相位信息，此时可以将信号通过两个相干检波器（即零中频混频器），分成两路，由于90°移相器的作用，使进入两个相干检波器的本振信号彼此相位差90°，信号被分成I、Q两路，这样信号的幅度和相位信息都保存下来了。同相分量和正交分量分别只占据原信号带宽的一半，采样率相应地也下降一半，但代价是需要两个A/D。原理框图如图4－1所示。

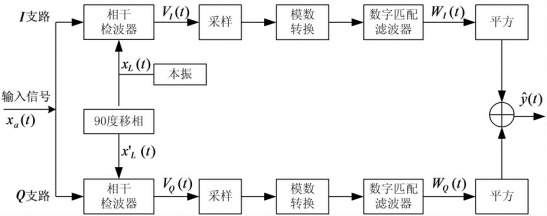
图4－1　零中频及I/Q正交通道

设输入信号为：

式中a（t）为信号的幅度调制，φ（t）为信号的相位调制。本振信号为：

相干检波器实际上是一乘法器和一低通滤波器之组合。因此I支路有：(www.xing528.com)

经低通滤波器，滤出2ω0的高频分量后得到：

Q支路经低通滤波器，滤出了2ω0的高频分量后得到：

I支路和Q支路在任意瞬间时，所得到的两个独立的幅值，既表达了该瞬间的信号幅度a（t），又表达了该瞬间的信号相位φ（t），即

当然以上讨论是基于理论上的，在实际的工程当中，由于两通道间不可避免地存在着不一致性，所以存在镜频误差，而且镜频抑制比很难超过30dB，这样的指标不能满足高性能雷达的要求。