脉冲压缩技术及线性调频的优势

由前面的分析可知，由于发射机的功率限制，短脉冲雷达虽然可以提供高的距离分辨率，但无法同时进行远距离探测。为了提高雷达系统的发现能力、测量精度和分辨能力，要求雷达信号具有大的时宽带宽和能量乘积。由于受到系统发射馈电设备的限制，大的信号能量也只有靠加大信号时宽来得到。通常的单载频脉冲信号的时宽带宽乘积接近于1，大的时宽带宽不可兼得，从而在测距、测速精度与分辨率以及作用距离等要求之间存在无法调和的矛盾。对大的时宽带宽积信号的需求，促成了基于匹配滤波的脉冲压缩技术的发展。在匹配滤波理论指导下，为了解决距离分辨率和探测距离的矛盾，往往通过频率和相位的调制来使长脉冲具有和短脉冲相当的带宽，从而提供了时宽和带宽乘积大于1的一种信号。这个处理过程我们称为脉冲压缩，脉冲压缩比定义为长脉冲与短脉冲的时宽比。而线性调频是最早的和发展最为成熟的脉冲压缩技术。

线性调频（LFM）信号是通过非线性相位调制来获得大的时宽和带宽。这种信号的突出优点是匹配滤波器对回波信号的多普勒频移不敏感，即使回波信号具有较大的多普勒频移，原来的匹配滤波器仍能起到良好的脉冲压缩作用。

一个典型的LFM波形可以表示为：

这里，f0为雷达中心频率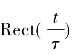，是一个宽度为τ的矩形脉冲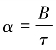，为扫频速率。可知，线性调频信号的幅度谱近似是一个矩形，而相位谱是一个平方相位项。可将式（2－32）写成载频和复包络u（t）的形式，即

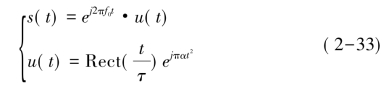
复包络的傅立叶变换为：

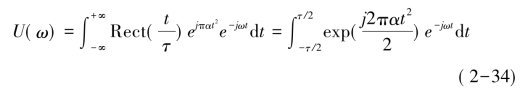
经过变量代换和菲涅耳（Fresnel）积分公式，可得：

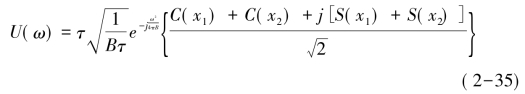
这里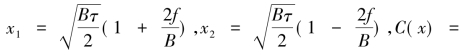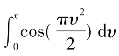，和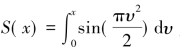为菲涅耳积分。根据菲涅耳积分的性质，当Bτ≫1时，Fresnel纹波很小，信号能量主要集中在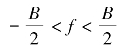范围内。随着时带积Bτ增大，LFM信号的振幅谱越接近矩形，匹配滤波效果越好，而相位残余项越接近恒定值因此在大Bτ值情况下，幅度谱和相位谱分别简化为：

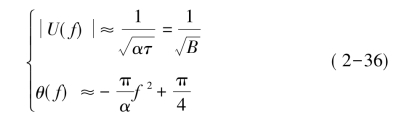
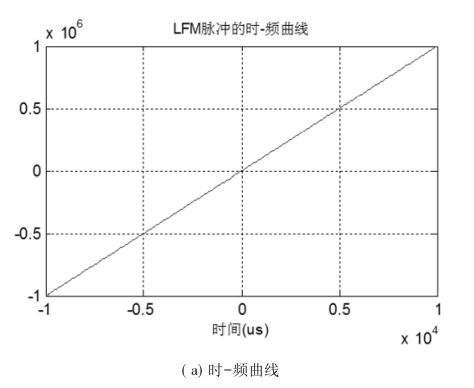
图2－2为带宽B=2MHz，时宽τ=20ms的LFM脉冲信号的波形图及频谱特性。

(www.xing528.com)

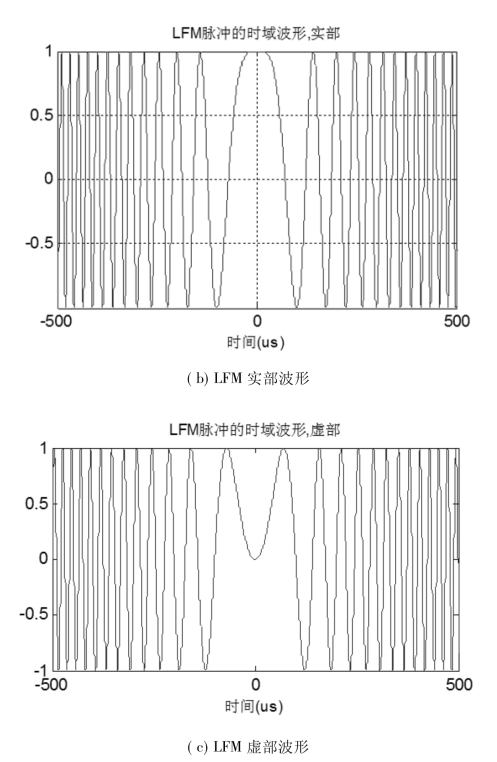
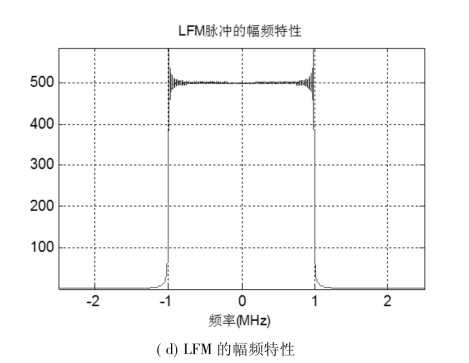
图2－2　LFM波形及频谱

因此，根据匹配滤波器理论：回波信号和匹配滤波器的单位冲激响应h（t）的幅度谱是一个相同的矩形，但相位相反。则滤波器的脉冲响应为：

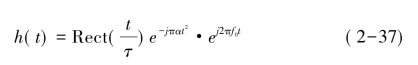
发射信号经过系统，由h（t）得输出信号y（t），即

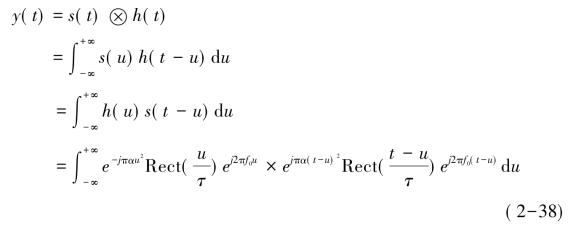
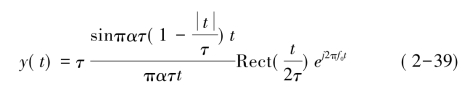
式（2－39）即为LFM脉冲信号经匹配滤波器的输出，它是一固定载频f0的信号。当t≤τ时，包络近似为辛格（Sinc）函数。

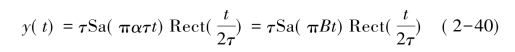
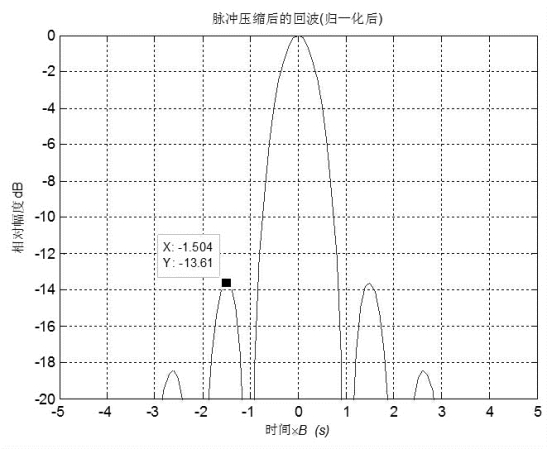
图2－3　LFM匹配滤波输出

线性调频信号的突出优点是匹配滤波器对回波信号的多普勒频移不敏感，即使回波信号有较大的多普勒频移，原来的匹配滤波器仍能起到脉冲压缩的作用，这将大大简化信号处理系统。但是，从图2－3可以看到，第一距离旁瓣只比主瓣低13．6dB，其他旁瓣随其离主瓣的间隔x按的规律衰减，旁瓣零点间间隔为。在多目标环境中，这些旁瓣会埋没附近较小目标的主信号，引起目标丢失。为了提高分辨多目标的能力，必须采用旁瓣抑制的方法，即加窗处理。加窗会导致信噪比损失，并使距离主瓣展宽。实验表明当采用海明（Hamming）窗加权时，最大旁瓣可减小到－42．8dB，只是信噪比损失1．34dB，主瓣展宽50%。为降低距离旁瓣导致的信噪比损失，通常可控制在1dB左右，这在目标检测中是容许的。