化与应用实例简介

1.PID控制器在连续控制系统中的表达式

PID是比例、积分、微分的缩写，PID控制器是应用最广的闭环控制器。模拟量PID控制器的输出表达式为

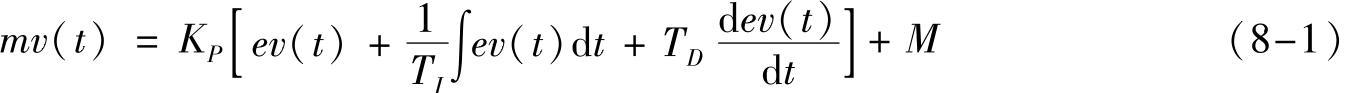
式中控制器的输入量（误差信号）为

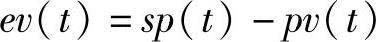
sp（t）为设定值，pv（t）为过程变量（反馈值）；mv（t）是控制器的输出信号，K_P为比例系数（FB41称为增益），T_I和T_D分别是积分时间和微分时间，M是积分部分的初始值。

式（8-1）中等号右边的前3项分别是比例、积分、微分部分，它们分别与误差ev（t）、误差的积分和误差的一阶导数成正比。如果取其中的一项或两项，可以组成P、PI或PD调节器。一般采用PI控制方式，控制对象的惯性滞后较大时，应采用PID控制方式。

控制器输出量中的比例、积分、微分部分都有明确的物理意义。

2.对比例控制作用的理解

PID的控制原理可以用人对炉温的手动控制来理解。假设用热电偶检测炉温，用数字式仪表显示温度值。在人工控制过程中，操作人员用眼睛读取炉温，并与炉温的设定值比较，得到温度的误差值。用手操作电位器，调节加热的电流，使炉温保持在设定值附近。有经验的操作人员通过手动操作可以得到很好的控制效果。

操作人员知道使炉温稳定在设定值时电位器的大致位置（我们将它称为位置L），并根据当时的温度误差值调整电位器的转角。炉温小于设定值时，误差为正，在位置L的基础上顺时针增大电位器的转角，以增大加热的电流；炉温大于设定值时，误差为负，在位置L的基础上反时针减小电位器的转角，以减小加热的电流。令调节后的电位器转角与位置L的差值与误差绝对值成正比，误差绝对值越大，调节的角度越大。上述控制策略就是比例控制，即PID控制器输出中的比例部分与误差成正比，比例系数（增益）为式（8-1）中的K_P。

闭环中存在着各种各样的延迟作用。例如调节电位器转角后，到温度上升到新的转角对应的稳态值有较大的延迟。温度的检测、模拟量转换为数字值和PID的周期性计算都有延迟。由于延迟因素的存在，调节电位器转角后不能马上看到调节的效果，因此闭环控制系统调节困难的主要原因是系统中的延迟作用。

如果增益太小，即调节后电位器转角与位置L的差值太小，调节的力度不够，将使温度的变化缓慢，调节时间过长。如果增益过大，即调节后电位器转角与位置L的差值过大，调节力度太强，造成调节过头，可能使温度忽高忽低，来回震荡。

与具有较大滞后的积分控制作用相比，比例控制作用与误差同步，在误差出现时，比例控制能立即起作用，使被控制量朝着误差减小的方向变化。

如果闭环系统没有积分作用（即系统为自动控制理论中的0型系统），由理论分析可知，单纯的比例控制有稳态误差，稳态误差与增益成反比。

图8-6和图8-7中的方波是比例控制的给定曲线，图8-6的系统增益小，超调量小，震荡次数少，但是稳态误差大。增益增大几倍后，启动时被控量的上升速度加快（见图8-7），稳态误差减小，但是超调量增大，振荡次数增加，调节时间加长，动态性能变坏。增益过大甚至会使闭环系统不稳定。因此单纯的比例控制很难兼顾动态性能和稳态性能。

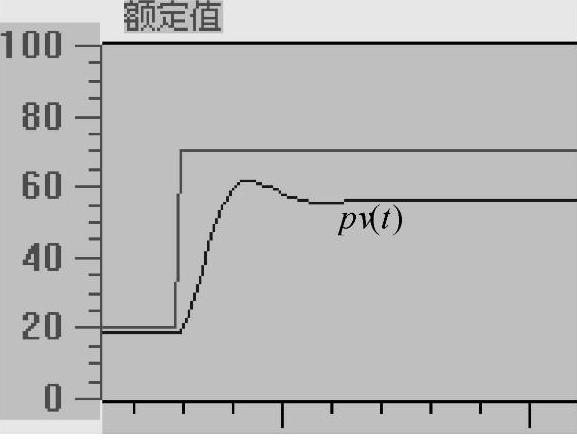
图8-6 比例控制的阶跃响应曲线

图8-7 比例控制的阶跃响应曲线

3.对积分控制作用的理解

（1）积分的几何意义与近似计算

PID程序是周期性执行的，执行PID程序的时间间隔为采样时间T_S。第n次PID运算时的时间为T_Sn，因为PID程序运行时T_S为常数，将t＝T_Sn时PID控制器的输入量ev（T_Sn）简写为ev（n），输出量mv（T_Sn）简写为mv（n）。

式（8-1）中的积分∫ev（t）dt对应于图8-8中误差曲线ev（t）与坐标轴包围的面积（图中的灰色部分）。我们只能使用连续的误差曲线上间隔时间为T_S的一些离散的点的值来计算积分，因此不可能计算出准确的积分值，只能对积分作近似计算。

一般用8-8图中的矩形面积之和来近似计算精确积分。每块矩形的面积为ev（jT_S）T_S。为了书写方便，将ev（jT_S）简写为ev（j），各块矩形的总面积为 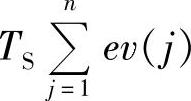。当T_S较小时积分的误差不大。可以理解为每次PID运算时，积分运算是在原来的积分值的基础上，增加一个与当前的误差值成正比的微小部分（对应于新增加的矩形面积）。在图8-9中A点和B点、C点和D点之间，设定值大于反馈值，误差为正，积分项增大。在B点和C点之间，反馈值大于设定值，误差为负，积分项减小。

图8-8 积分的近似运算

（2）积分控制的作用

在上述的温度控制系统中，积分控制相当于根据当时的误差值，周期性地微调电位器的角度。温度低于设定值时误差为正，积分项增大一点点，使加热电流增加；反之积分项减小一点点。只要误差不为零，控制器的输出就会因为积分作用而不断变化。积分这种微调的“大方向”是正确的，因此积分项有减小误差的作用。只要误差不为零，积分项就会向减小误差的方向变化。在误差很小的时候，比例部分和微分部分的作用几乎可以忽略不计，但是积分项仍然不断变化，用“水滴石穿”的力量，使误差趋近于零。

在系统处于稳定状态时，误差恒为零，比例部分和微分部分均为零，积分部分不再变化，并且刚好等于稳态时需要的控制器的输出值，对应于上述温度控制系统中电位器转角的位置L。因此积分部分的作用是消除稳态误差，提高控制精度，积分作用一般是必需的。在纯比例控制的基础上增加积分控制（即PI控制），被控量最终等于设定值（见图8-10），稳态误差被消除。

图8-9 PID控制器输出中的积分分量

图8-10 PI控制器的阶跃响应曲线

（3）积分控制的缺点

积分项与当前误差值和过去的历次误差值的累加值成正比，因此积分作用具有严重的滞后特性，对系统的稳定性不利。如果积分时间设置得不好，其负面作用很难通过积分作用迅速地修正。如果积分作用太强，相当于每次微调电位器的角度值过大。其累积的作用与增益过大相同，会使系统的动态性能变差，超调量增大，甚至使系统不稳定。积分作用太弱，则消除误差的速度太慢。(www.xing528.com)

（4）积分控制的应用

PID的比例部分没有延迟，只要误差一出现，比例部分就会立即起作用。具有滞后特性的积分作用很少单独使用，它一般与比例控制和微分控制联合使用，组成PI或PID控制器。

PI和PID控制器既克服了单纯的比例调节有稳态误差的缺点，又避免了单纯的积分调节响应慢、动态性能不好的缺点，因此被广泛使用。如果控制器有积分作用（例如采用PI或PID控制），积分能消除阶跃输入的稳态误差，这时可以将增益调得小一些。

（5）积分部分的调试

因为积分时间T_I在式（8-1）的积分项的分母中，T_I越小，积分项变化的速度越快，积分作用越强。综上所述，积分作用太强（即T_I太小），系统的稳定性变差，超调量增大。积分作用太弱（即T_I太大），系统消除稳态误差的速度太慢，T_I的值应取得适中。

4.对微分控制作用的理解

（1）微分的几何意义与近似计算

在误差曲线ev（t）上作一条切线（见图8-11），该切线与x轴正方向的夹角α的正切值tanα即为该点处误差的一阶导数dev（t）/dt。PID控制器输出表达式（8-1）中的导数用下式来近似：

式中，ev（n-1）（见图8-11）是第n-1次采样时的误差值。将积分和导数的近似表达式代入式（8-1），第n次采样时控制器的输出为

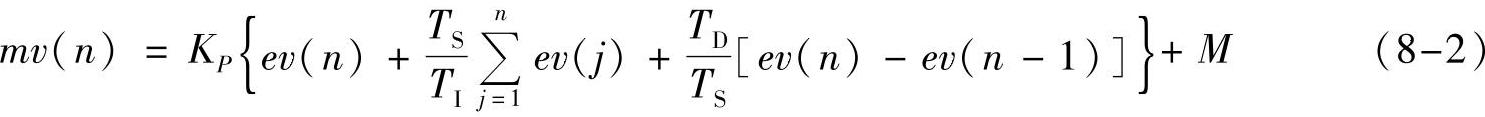
在FB41“CONT_C”（连续控制器）中，K_P、T_I、T_D和M分别对应于输入参数GAIN、TI、TD和积分初始值I_ITLVAL。

（2）微分部分的物理意义

PID输出的微分分量与误差的变化速率（即导数）成正比，误差变化越快，微分分量的绝对值越大。微分分量的符号反映了误差变化的方向。在图8-12的A点和B点之间、C点和D点之间，误差不断减小，微分分量为负；在B点和C点之间，误差不断增大，微分分量为正。控制器输出量的微分部分反映了被控量变化的趋势。

有经验的操作人员在温度上升过快，但是尚未达到设定值时，根据温度变化的趋势，预感到温度将会超过设定值，出现超调。于是调节电位器的转角，提前减小加热的电流。这相当于士兵射击远方的移动目标时，考虑到子弹运动的时间，需要一定的提前量一样。

图8-11 微分的近似计算

图8-12 PID控制器输出中的微分分量

在图8-12中启动过程的上升阶段（A点到E点），被控量尚未超过其稳态值，超调还没有出现。但是因为被控量不断增大，误差e（t）不断减小，误差的导数和控制器输出量的微分分量为负，使控制器的输出量减小，相当于减小了温度控制系统的加热功率，提前给出了制动作用，以阻止温度上升过快，所以可以减小超调量。因此微分控制具有超前和预测的特性，在温度尚未超过稳态值之前，根据被控量变化的趋势，微分作用就能提前采取措施，以减小超调量。在图8-12的E点和B点之间，被控量继续增大，控制器输出量的微分分量仍然为负，继续起制动作用，以减小超调量。

闭环控制系统的振荡甚至不稳定的根本原因在于有较大的滞后因素，因为微分分量能预测误差变化的趋势，微分控制的超前作用可以抵消滞后因素的影响。适当的微分控制作用可以使超调量减小，调节时间缩短，增加系统的稳定性。对于有较大惯性或滞后的被控对象，控制器输出量变化后，要经过较长的时间才能引起反馈值的变化。如果PI控制器的控制效果不理想，可以考虑在控制器中增加微分作用，以改善闭环系统的动态特性。

（3）微分部分的调试

微分时间T_D与微分作用的强弱成正比，T_D越大，微分作用越强。微分作用的本质是阻碍被控量的变化，如果微分作用太强（T_D太大），对误差的变化压抑过度，将会使响应曲线变化迟缓，超调量反而可能增大（见图8-22）。此外微分部分过强会使系统抑制干扰噪声的能力降低。综上所述，微分控制作用的强度应适当，太弱则作用不大，过强则有负面作用。如果将微分时间设置为0，微分部分将不起作用。

（4）不完全微分PID

微分作用的引入可以改善系统的动态性能，其缺点是对干扰噪声敏感，使系统抑制干扰的能力降低。为此在微分部分增加一阶惯性滤波环节，以平缓PID控制器输出中微分部分的剧烈变化。这种PID称为不完全微分PID。

设惯性滤波环节的时间常数为T_f，不完全微分PID的传递函数为

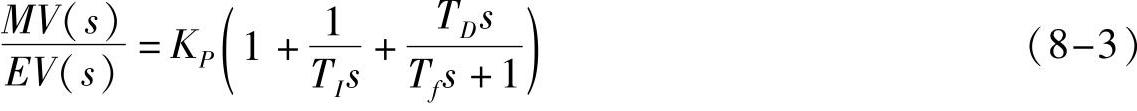
在FB41中，T_f对应于微分操作的延迟时间TM_LAG。闲环仿真发现，如果采用了不完全微分PID，当T_D和T_f太大时，将会使响应曲线变得很怪异，甚至会出现“毛刺”。

5.怎样实现PID控制

S7-300的FM 355和S7-400的FM 455是智能化的4路和16路通用闭环控制模块，它们集成了闭环控制需要的I/O点和软件，FM 455提供了PID算法和自优化温度控制算法。

PID控制模块的价格较高，因此一般使用普通的信号模块和PID控制功能块（FB）来实现PID控制。所有型号的CPU都可以使用PID控制功能块FB41～FB43，和用于温度闭环控制的FB58和FB59，它们在程序编辑器左边窗口的文件夹“\库\Standard Library（标准库）\PID Control-ler（PID控制器）”中。FB41～FB43除了PID控制器功能以外，还可以处理设定值和过程反馈值，以及对控制器的输出值进行后期处理。计算所需的数据保存在指定的背景数据块中。

FB41“CONT_C”（连续控制器）输出的数字值一般用AO模块转换为连续的模拟量。

FB43（脉冲发生器）与FB41组合，可以产生脉冲宽度调制的开关量输出信号，来控制比例执行机构，例如可以用于加热和冷却控制。FB42“CONT_S”用于步进控制，其特点是可以直接用它的两点开关量输出信号控制电动阀门，从而省去了电动调节阀内部的位置闭环控制器和位置传感器。FB42和FB43的应用实例见参考文献[1]。

实际控制中FB41用得最多，FB43用得较少，FB42用得很少。CPU 31xC还可以使用集成在CPU中与FB41～FB43兼容的SFB41～SFB43。

FB58（连续温度控制）和FB59（温度步进控制）有参数自整定功能，FB41和FB42则需要安装软件PID Self Tuner来实现在线的参数自整定