8.28 已知两耦合线圈L1=0.0625H,L2=0.04H,M=0.03H,试求其耦合系数K。
解: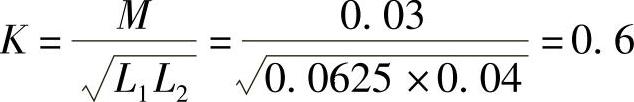
8.29 已知互感线圈L1=0.4H,L2=0.1H,互感系数M=0.08H,试求耦合系数K。若该互感线圈为全耦合时,互感系数M将变为多少?
解: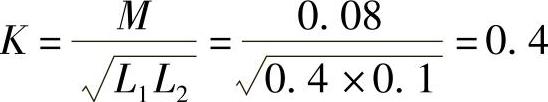
互感线圈为全耦合时,K′=1,则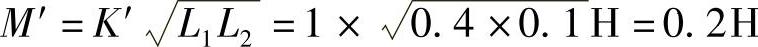
8.30 已知互感线圈如图8-33所示,试标出同名端。

图8-33 习题8.30互感线圈
解:利用右手螺旋法则,判得同名端如图8-33所示。
8.31 已知互感线圈如图8-34所示,试标出同名端。
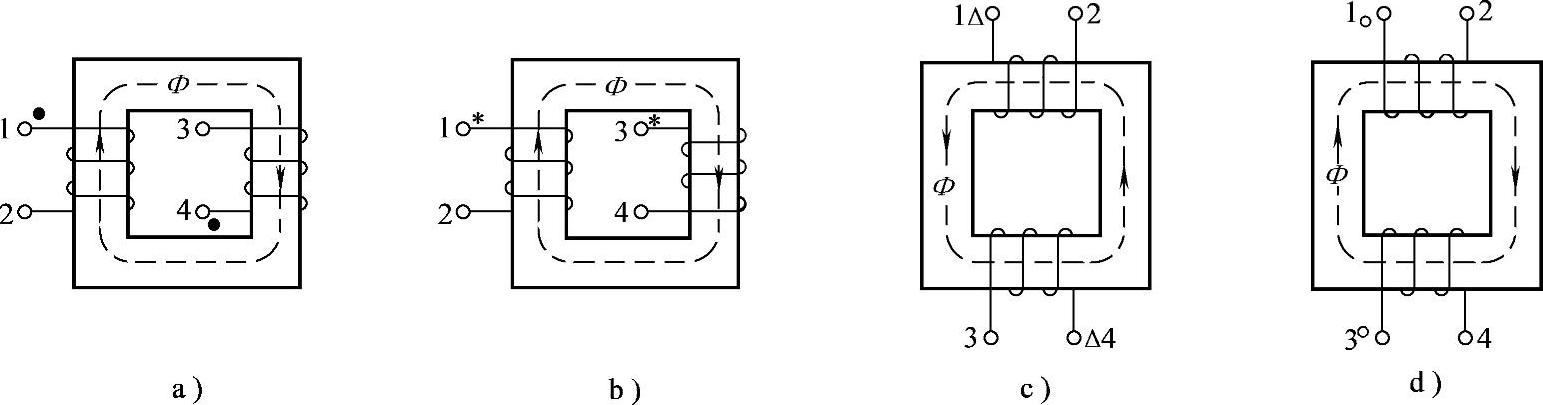
图8-34 习题8.31电路
解:利用右手螺旋法则,判得同名端如图8-34所示。其中虚线所示为电流从同名端流进时产生的磁通。
8.32 已知互感线圈如图8-35所示,试分别判断并标记同名端。
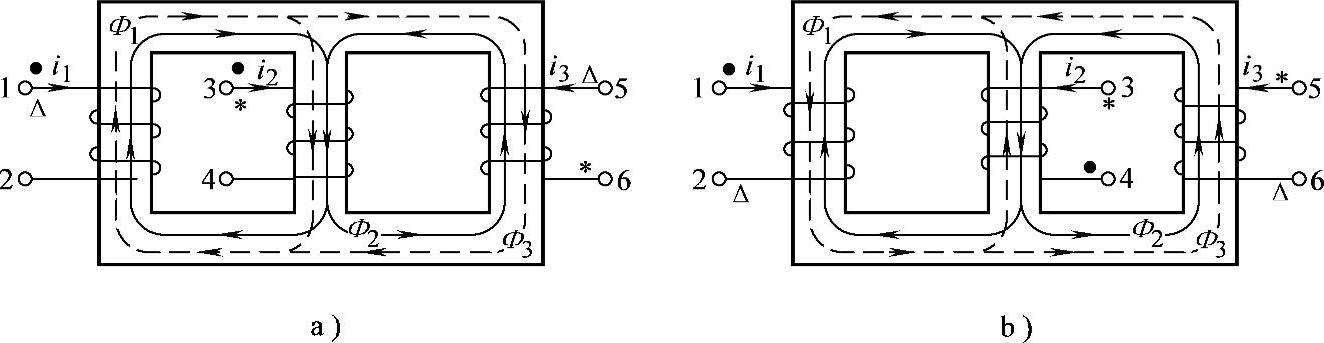
图8-35 习题8.32电路
解:图8-35a中,设线圈L1的电流i1从1端流进,按右手螺旋法则,产生磁通Φ1(用虚线表示),构成磁路时,在L1中方向向上,在铁心中的另两个分支,即L2和L3中方向均向下。现假设L2中电流i2从3端流进,产生的磁通Φ2(用实线表示)与Φ1方向相同,则1、3端为同名端,用“·”表示。再假设L3中电流i3从5端流进,产生的磁通Φ3与Φ1方向相同,则1、5端为同名端,用“△”表示。
具有分支的磁路,若绕有三个或三个以上互感线圈时,应每两个互感线圈间分别判断。L2与L3之间的同名端应按右手螺旋法则,重新判定。L2中电流i2从3端流进,产生的磁通Φ2(用实线表示),构成磁路时,在L3中方向向上;则L3中的电流i3必须从6端流进,才能产生与Φ2方向相同的磁通,因此3、6端为同名端,用“∗”表示。
图8-35b中,设线圈L1的电流i1从1端流进,按右手螺旋法则,产生磁通Φ1(用虚线表示),构成磁路时,在L1中方向向下,在铁芯中的另两个分支,即L2和L3中方向均向上。现假设L2中电流i2从3端流进,产生的磁通Φ2(用实线表示)与Φ1方向相反,则1、4端为同名端,用“·”表示。再假设L3中电流i3从5端流进,产生的磁通Φ3与Φ1方向相同,则1、5端为同名端(实际标为2、6端),用“△”表示。
L2与L3之间的同名端应按右手螺旋法则,重新判定。设L2中电流i2从3端流进,产生的磁通Φ2(用实线表示),构成磁路时,在L3中方向向上;则L3中的电流i3必须从5端流进,才能产生与Φ2方向相同的磁通,因此3、5端为同名端,用“∗”表示。
8.33 已知自感线圈L1、L2连接电路如图8-36所示,S开关合上瞬间,电压表指针反偏,试标出L1、L2同名端。
解:S开关合上瞬间,1端为正极性端。若电压表指针反偏,表明4端为正极性端,因此1、4端为同名端。
8.34 已知电路如图8-37所示,开关闭合瞬间,表指针反偏,试标出同名端。
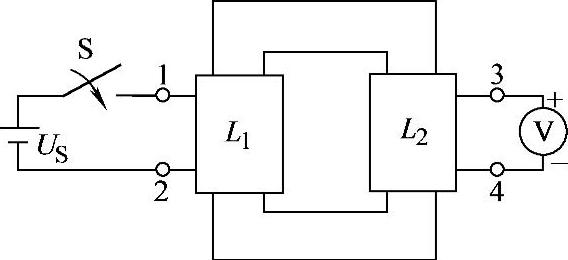
图8-36 习题8.33自感线圈
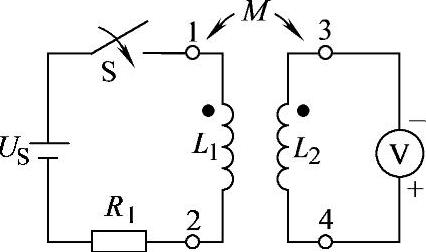
图8-37 习题8.34电路
解:标出同名端如图8-37所示。S闭合瞬间,L1的1端为正极性端;而图中电压表参考极性下正上负,指针反偏,表明电流从上向下流入电压表,L2的3端为正极性端,因此1、3端为同名端。
8.35 已知电路:图8-38a中,i1>0,i2>0,产生的磁通相互加强;图8-38b中,i1<0,i2>0,且产生的磁通相互减弱;试分别标出同名端。
解:标出同名端如图8-38所示。
图8-38a中,i1>0,i2>0,表明电流i1、i2的参考方向与实际方向一致。若此时产生的磁通相互增强,表明电流流进线圈端为同名端,即1、4端为同名端。
图8-38b中,i1<0,表明电流参考方向与实际方向相反,若此时产生的磁通相互减弱,表明实际电流流进端不是同名端,即1、3端为同名端。
8.36 已知互感电路如图8-39所示,M=0.1H,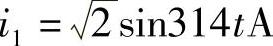 ,试求互感电压u21。
,试求互感电压u21。
解: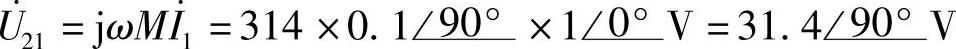
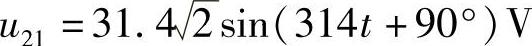
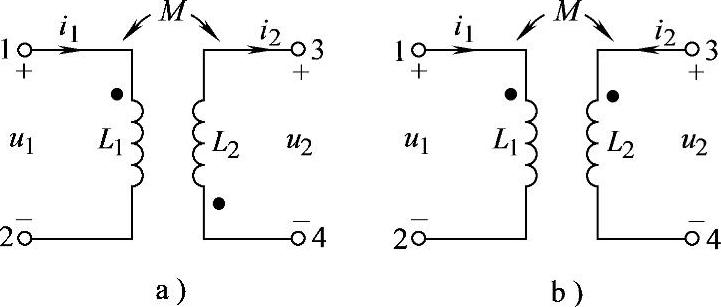
图8-38 习题8.35电路
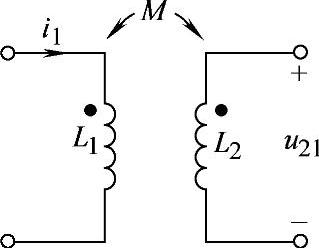
图8-39 习题8.36电路
8.37 已知互感电路如图8-40所示,试写出u1、u2表达式。
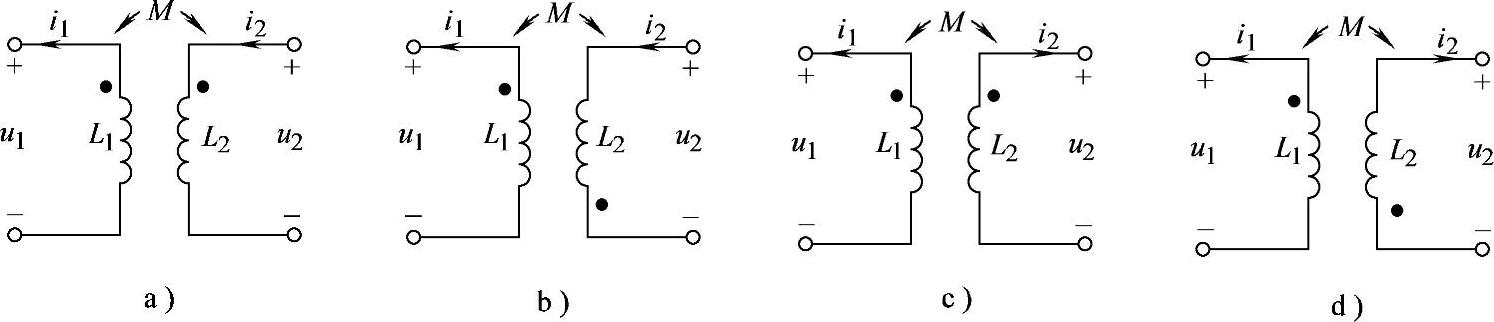
图8-40 习题8.37电路
解:参阅例8-2。
8.38 电路同上题,若激励源为正弦量,试写出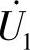 、
、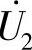 表达式。
表达式。
解:参阅例8-2。
8.39 已知电路如图8-41所示,ω=314rad/s,电流表和电压表读数分别为2A和220V,试求互感线圈的互感系数M。
解:图8-41中,uo端虽然接电压表,但电压表内阻很大,相当于uo端开路,电压表读数为uo开路电压。
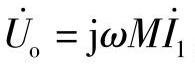 ,
,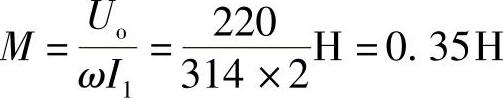
8.40 试画出图8-40中各互感耦合电路的受控源等效电路。
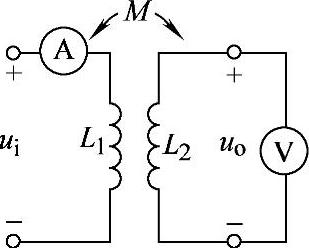
图8-41 习题8.39电路
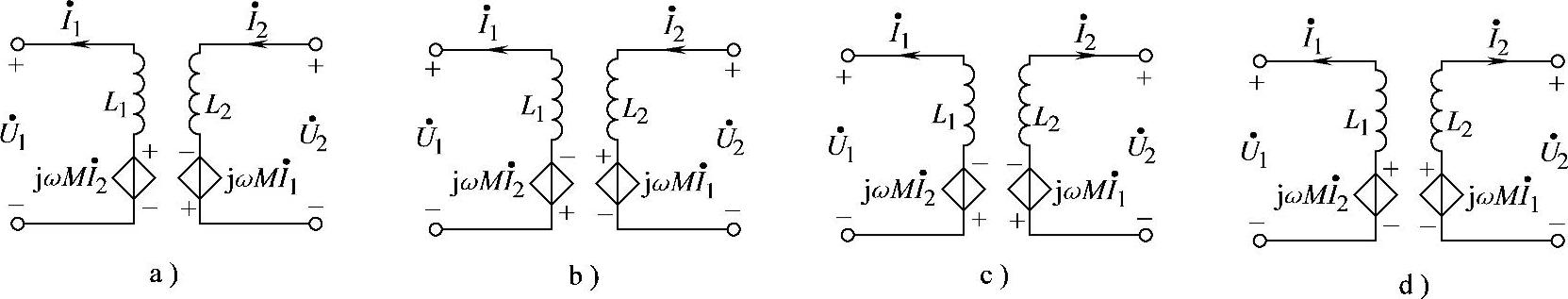
图8-42 习题8.40受控源等效电路
解:图8-40所示各电路的受控源等效电路分别如图8-42所示。
8.41 已知两互感线圈L1=5H,L2=4H,M=1H,试分别计算其同名端顺串和反串时的等效电感。
解:LF=L1+L2+2M=(5+4+2×1)H=11H
LR=L1+L2-2M=(5+4-2×1)H=7H
8.42 已知互感耦合线圈同名端顺向串联和反向串联电路分别如图8-43a、b所示,外施电压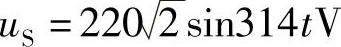 ,测得顺向串联时电流为I1=2.7A,电源提供功率为P=218.7W,反向串联时电流为I2=7A,试求互感系数M。
,测得顺向串联时电流为I1=2.7A,电源提供功率为P=218.7W,反向串联时电流为I2=7A,试求互感系数M。
解:电源提供功率为互感线圈电阻R=R1+R2消耗功率。
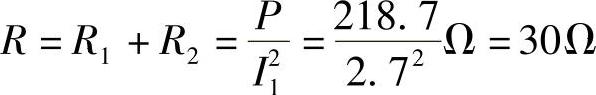
顺串时阻抗: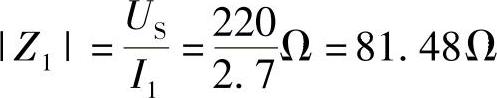
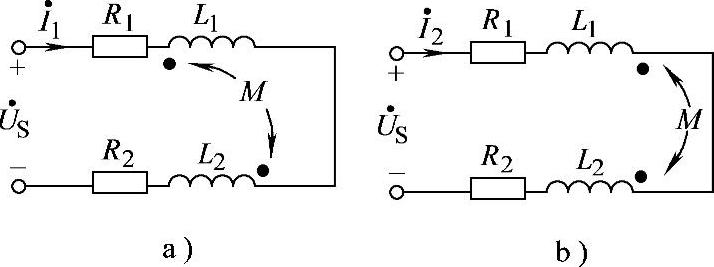
图8-43 习题8.42电路
感抗: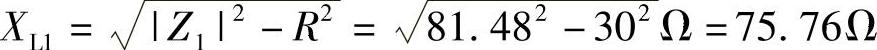
等效电感: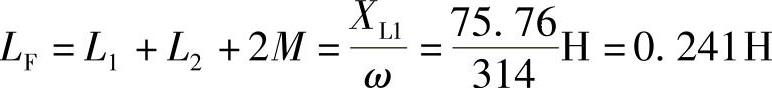
反串时阻抗: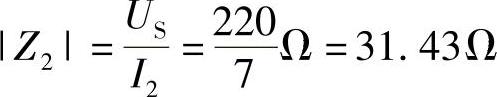
感抗: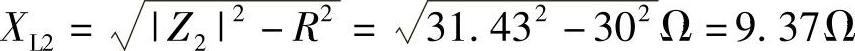
等效电感: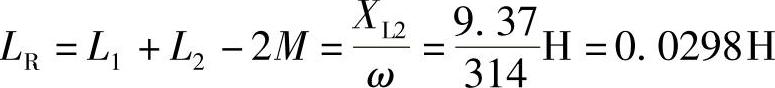
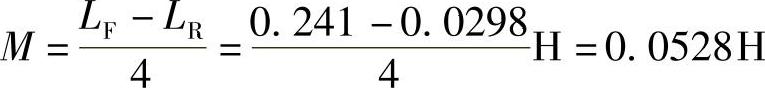
8.43 某互感耦合线圈AB和CD为全密封,对外仅引出4个接线端A、B、C、D。若将B、C端短接,测得A、D端电感量为10H;若将B、D端短接,测得A、C端电感量为6H。试指出其同名端,并求互感系数M。
解:根据互感线圈同名端顺向串联等效电感LF大于反向串联等效电感LR的特性,可得出A、C端为同名端。
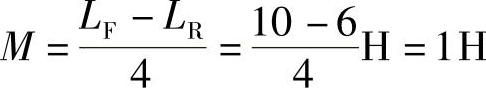
8.44 已知互感电路如图8-44a所示,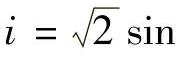
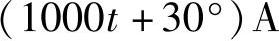 ,M=0.01H,L1=L2=0.02H,试求
,M=0.01H,L1=L2=0.02H,试求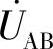 ,并画出
,并画出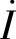 、
、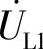 、
、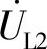 、
、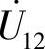 、
、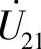 和
和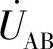 相量图。
相量图。
解: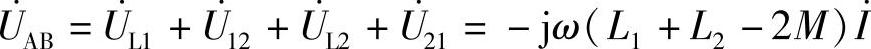
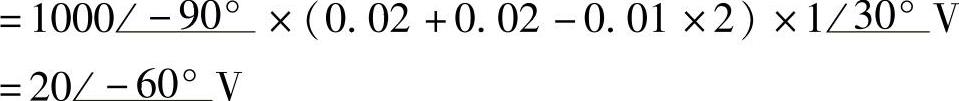
据此,画出相量图如图8-44b所示,其中UL1=UL2,U21=U12。
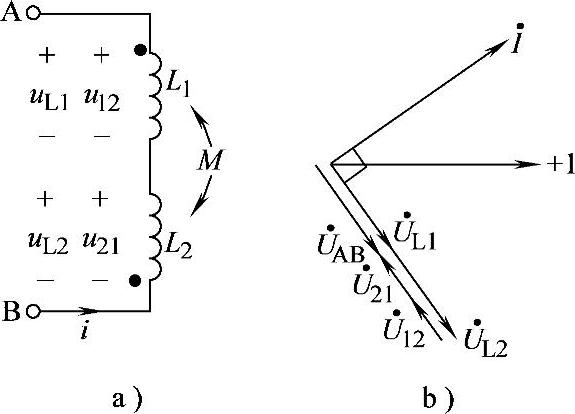
图8-44 习题8.44电路和相量图
8.45 已知互感电路如图8-45所示,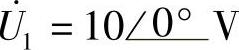 ,ωL1=ωL2=4Ω,ωM=2Ω,试求开路电压
,ωL1=ωL2=4Ω,ωM=2Ω,试求开路电压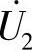 。
。
解:因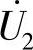 输出端开路,故
输出端开路,故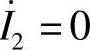 ,因此:
,因此: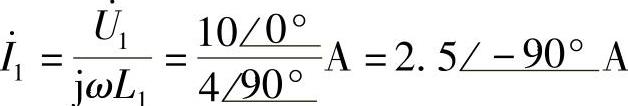
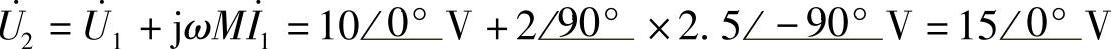
8.46 已知互感电路如图8-46所示,R1=4Ω,R2=6Ω,ωL1=5.5Ω,ωL2=8.5Ω,ωM=3Ω,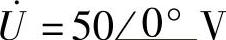 ,试求电流
,试求电流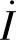 。
。
解:图8-46中,互感线圈同名端顺向串联。因此
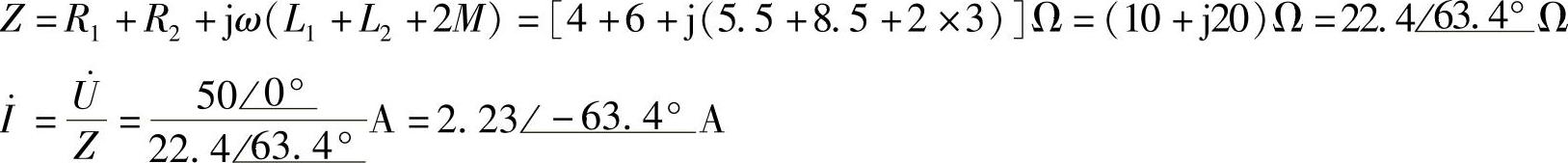
8.47 已知互感电路如图8-47所示,R1=3Ω,R2=7Ω,ωL1=9.5Ω,ωL2=10.5Ω,ωM=5Ω,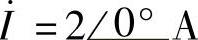 ,试求电压
,试求电压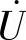 。
。
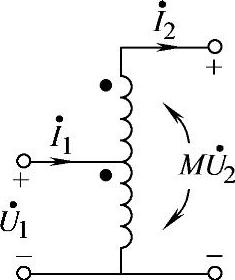
图8-45 习题8.45电路
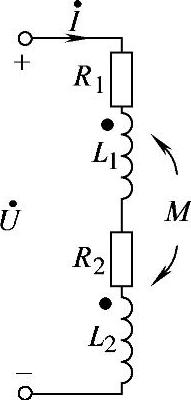
图8-46 习题8.46电路
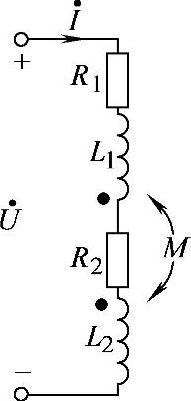
图8-47 习题8.47电路
解:图8-47中,互感线圈同名端反向串联。因此
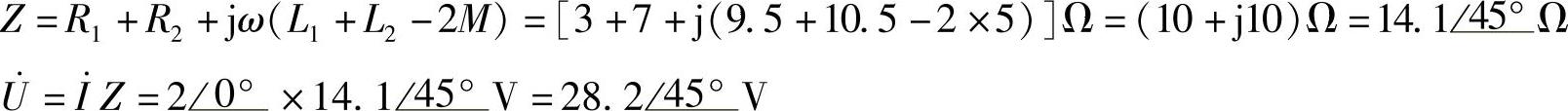
8.48 已知互感电路如图8-48所示,R1=R2=3Ω,ωL1=ωL2=6Ω,ωM=2Ω,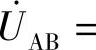
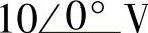 ,输出端CB开路,试求当互感线圈同名端顺向串联和反向串联时的
,输出端CB开路,试求当互感线圈同名端顺向串联和反向串联时的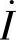 、
、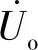 。
。
解:参阅例8-4。
8.49 已知互感电路如图8-49所示,R=100Ω,L1=0.1H,L2=0.4H,K=0.5,C=10pF,试求电路谐振时谐振频率f0。
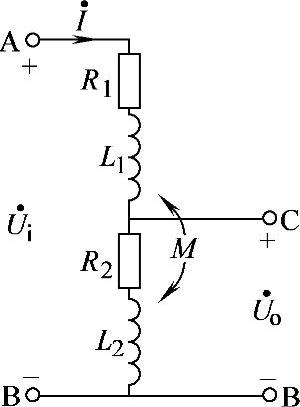
图8-48 习题8.48电路
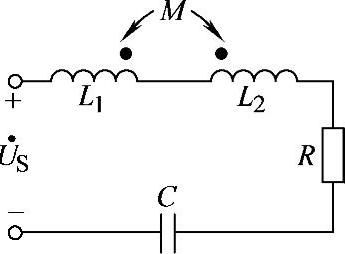
图8-49 习题8.49电路
解: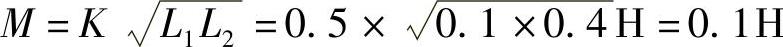
互感线圈同名端反向串联等效电感:
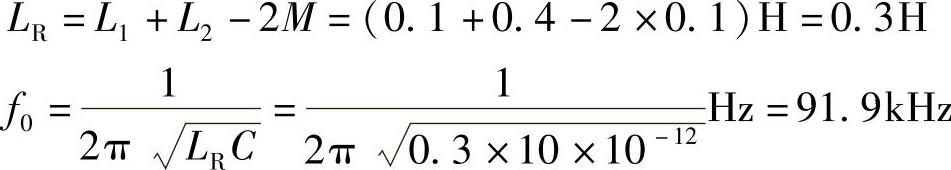
8.50 已知互感线圈一端相联电路如图8-50a、b所示,试画出其去耦等效电路。

图8-50 习题8.50电路
解:图8-50a互感线圈同侧一端相联时,去耦等效电路如图8-50c所示;
图8-50b互感线圈异侧一端相联时,去耦等效电路如图8-50d所示;
8.51 已知互感电路如图8-51a所示,R1=3Ω,R2=5Ω,ωL1=7.5Ω,ωL2=12.5Ω,ωM=6Ω,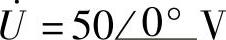 ,试求S开关断开和闭合时的电流
,试求S开关断开和闭合时的电流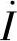 。
。
解:(1)S开关断开时:
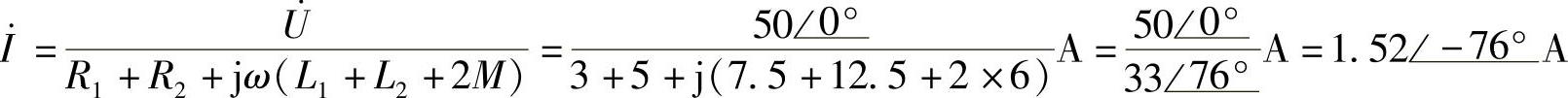
(2)S开关闭合时,画出其去耦等效电路如图8-51b所示。
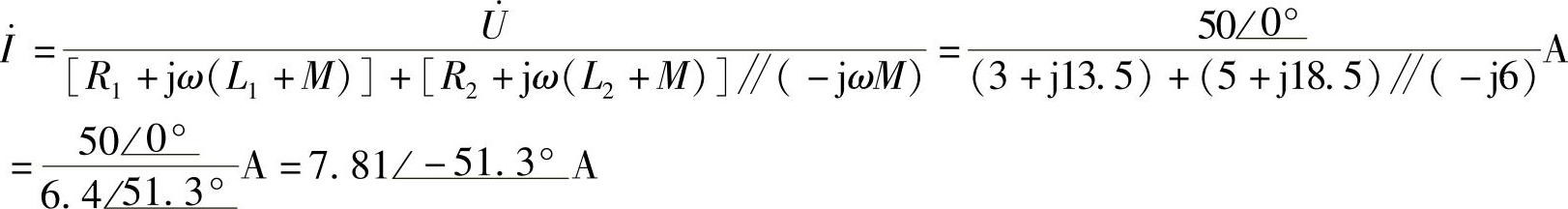
8.52 已知互感电路如图8-52a所示,R1=3Ω,R2=6Ω,XL1=21Ω,XL2=30Ω,ωM=5Ω,XC=4Ω,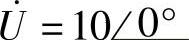 ,试求电路输入电阻Z和电流
,试求电路输入电阻Z和电流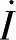 。
。
解:参阅例8-5。
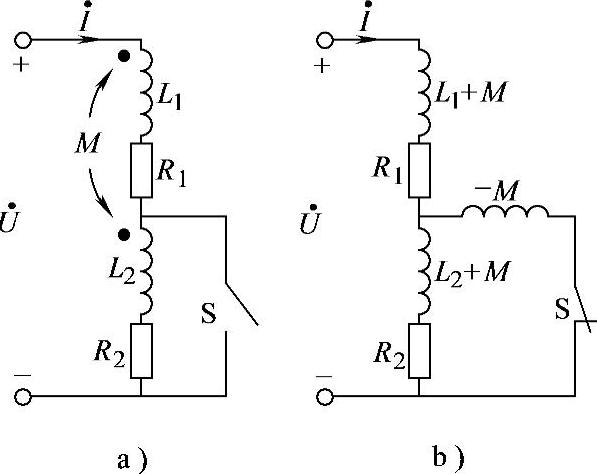
图8-51 习题8.51电路
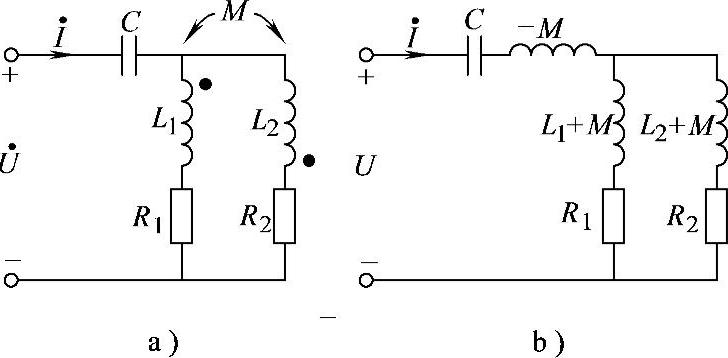
图8-52 习题8.52电路
8.53 已知互感电路如图8-53a所示,R1=R2=6Ω,ωL1=ωL2=10Ω,ωM=5Ω,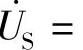
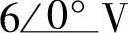 ,试求AB端戴维南等效电路。
,试求AB端戴维南等效电路。
解:电路为同名端同侧一端相连互感电路,画出其去耦等效电路如图8-53b所示。
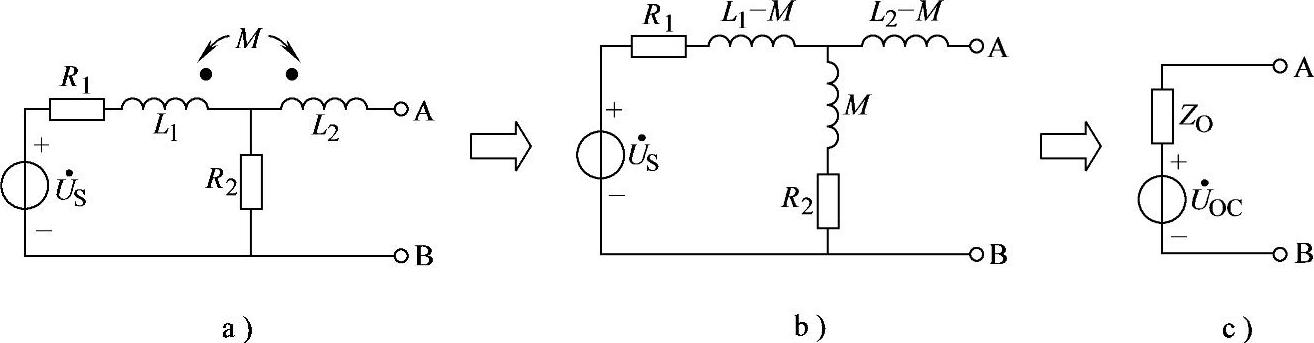
图8-53 习题8.53电路
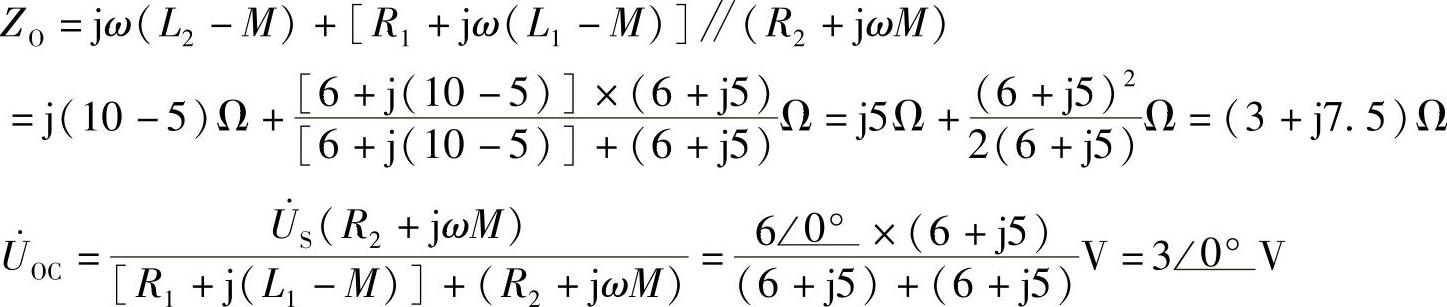
画出戴维南等效电路如图8-53c所示,其中ZO=(3+j7.5)Ω,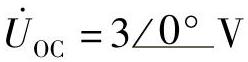 (https://www.xing528.com)
(https://www.xing528.com)
8.54 已知互感电路如图8-54a所示,R1=R2=1Ω,ωL1=3Ω,ωL2=2Ω,ωM=2Ω,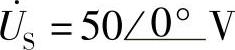 ,试求S开关断开和闭合时
,试求S开关断开和闭合时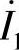 。
。
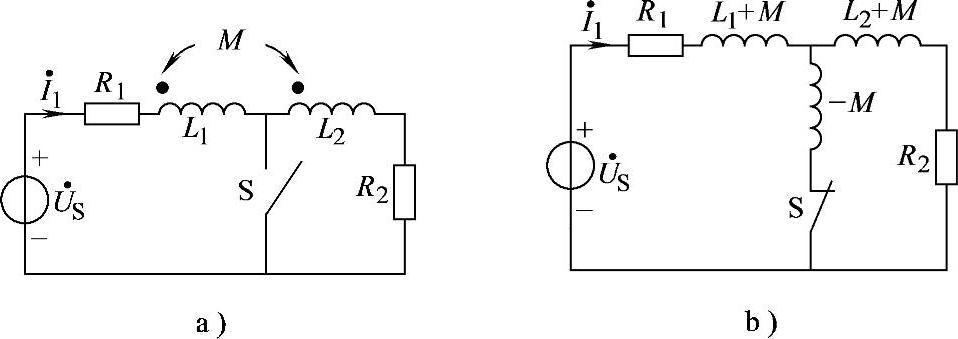
图8-54 习题8.54电路
解:(1)S断开时:
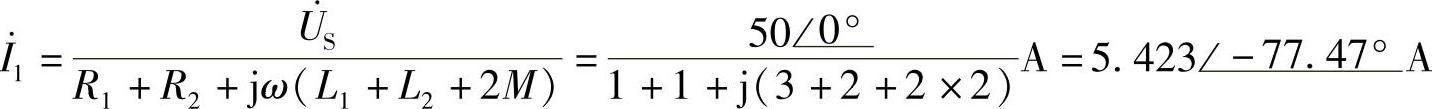
(2)S闭合时,去耦等效电路如图8-54b所示。
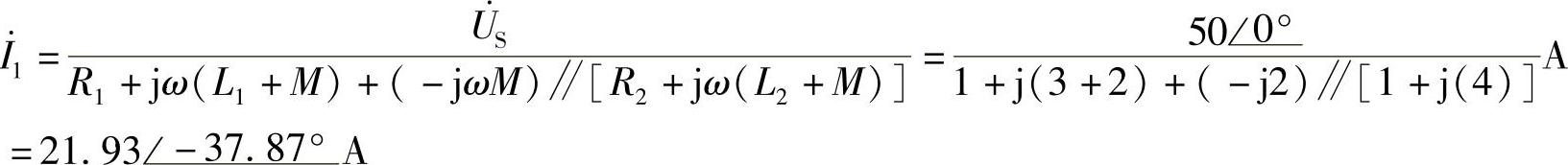
8.55 已知两互感线圈L1=5H,L2=3H,M=2H,试分别计算其同名端同侧并联和异侧并联时的等效电感。
解:同侧并联: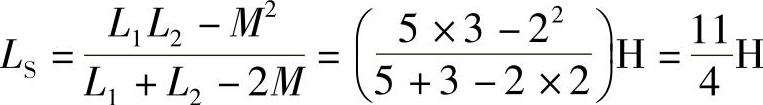
异侧并联: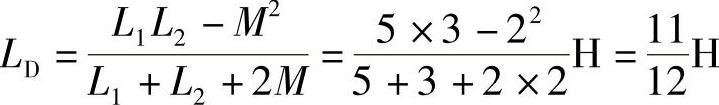
8.56 已知互感电路如图8-55所示,L1=0.1H,L2=0.2H,M=0.1H,C=10μF,试求电路谐振角频率ω0。
解:同名端异侧并联时的等效电感:

8.57 已知互感电路如图8-56所示,R=10Ω,L1=0.2H,L2=0.4H,M=0.1H,C=5pF,试求电路谐振时振荡角频率ω0。
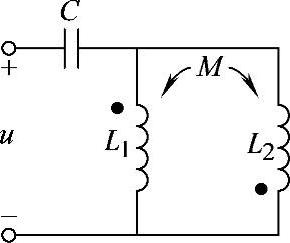
图8-55 习题8.56电路
解:互感线圈同名端同侧并联等效电感:
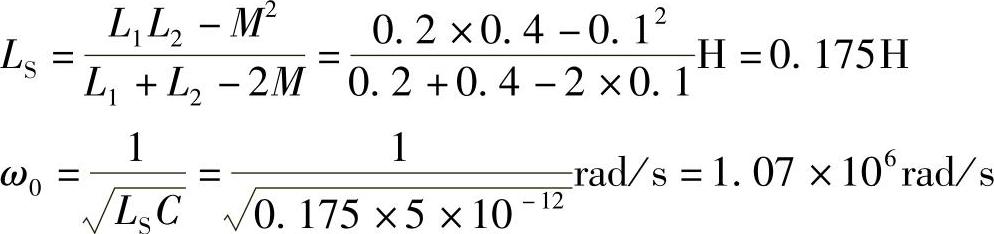
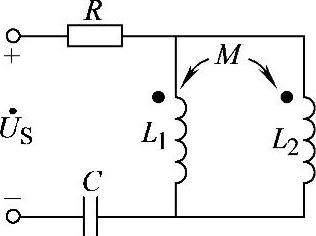
图8-56 习题8.57电路
8.58 已知互感电路如图8-57所示,电路两端电压u相同, >
> ,
, >
> ,试标出互感线圈同名端。
,试标出互感线圈同名端。
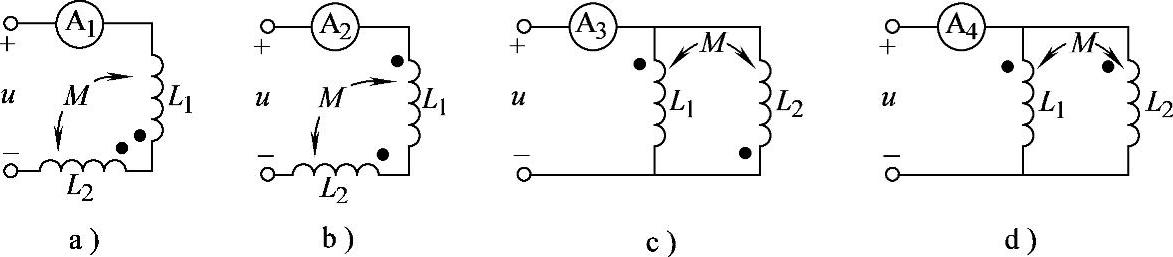
图8-57 习题8.58电路
解:图8-57a、b电路, >
> ,表明Z1<Z2,即图8-57a为互感同名端反向串联,图8-57b为互感同名端顺向串联。
,表明Z1<Z2,即图8-57a为互感同名端反向串联,图8-57b为互感同名端顺向串联。
图8-57c、d电路, >
> ,表明Z3<Z4,即图8-57c为互感同名端异侧并联,图8-57d为互感同名端同侧并联。
,表明Z3<Z4,即图8-57c为互感同名端异侧并联,图8-57d为互感同名端同侧并联。
标出同名端如图8-57所示。
8.59 已知电路如图8-58所示,L1=0.1H,L2=0.4H,M=0.12H,试求:(1)CD端短路时,AB端等效电感LAB;(2)AB端短路时,CD端等效电感LCD。
解:(1)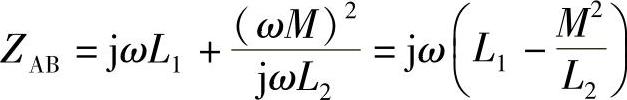
等效电感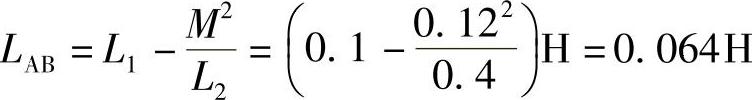
(2)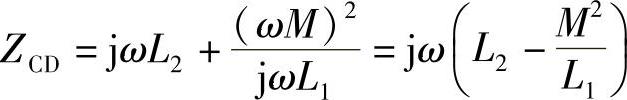
等效电感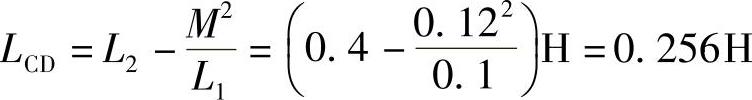
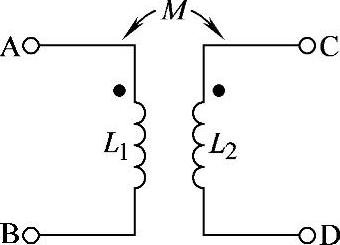
图8-58 习题8.59电路
8.60 已知电路如图8-59所示,L1=6H,L2=4H,M=3H,ω=100rad/s,试求:(1)CD端短路时AB端输入阻抗Z1;(2)AB端短路时CD端输入阻抗Z2;(3)若L1、L2同名端与图8-59中相反,再求Z1、Z2。
解:(1)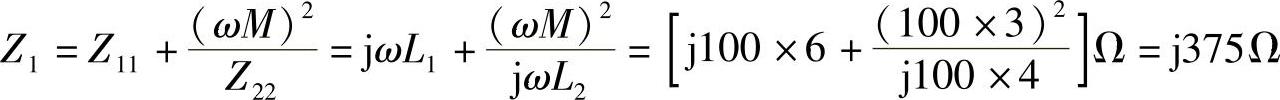
(2)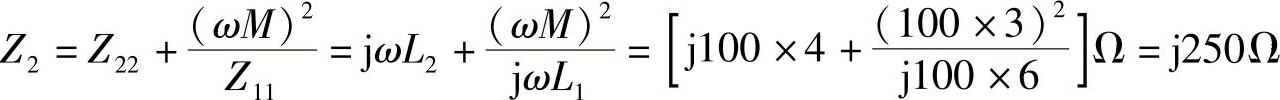
(3)L1、L2同名端取反,并不影响反射阻抗计算。
8.61 已知电路如图8-60所示,R1=6Ω,ωL1=8Ω,ωL2=ωM=2Ω,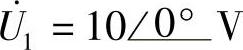 ,试求:
,试求:
(1)S开关断开时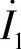 和
和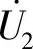 ;(2)S开关闭合时
;(2)S开关闭合时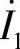 和
和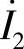 。
。
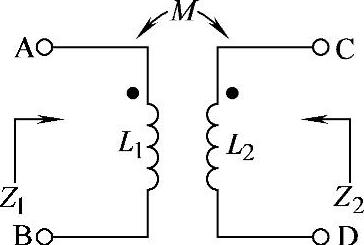
图8-59 习题8.60电路
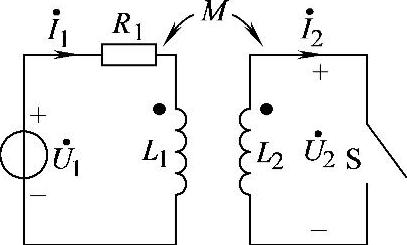
图8-60 习题8.61电路
解:(1)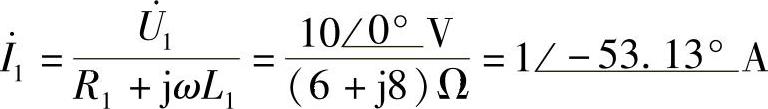
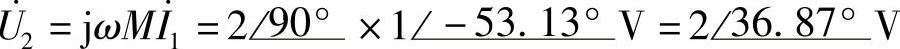
(2)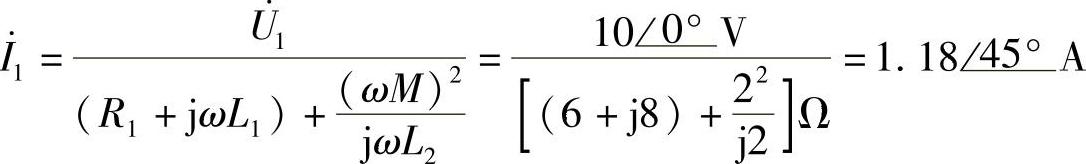
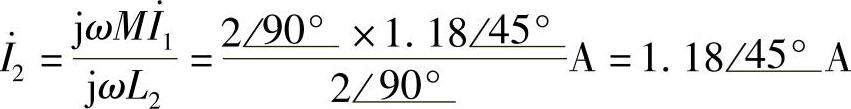
8.62 已知电路如图8-61所示,L1=10H,L2=2.4H,M=2H,R=10Ω,ω=10rad/s,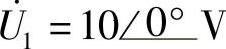 ,试求二次线圈电流
,试求二次线圈电流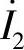 。
。
解:参阅例8-6。
8.63 已知电路如图8-62a所示,R1=20Ω,R2=0.08Ω,L1=3.6H,L2=0.06H,M=0.465H,RL=42Ω,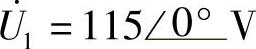 ,ω=314rad/s,试求
,ω=314rad/s,试求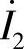 。
。
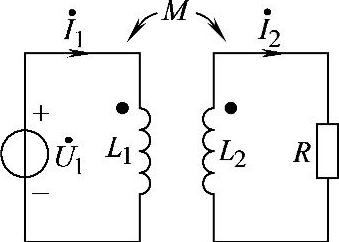
图8-61 习题8.62电路
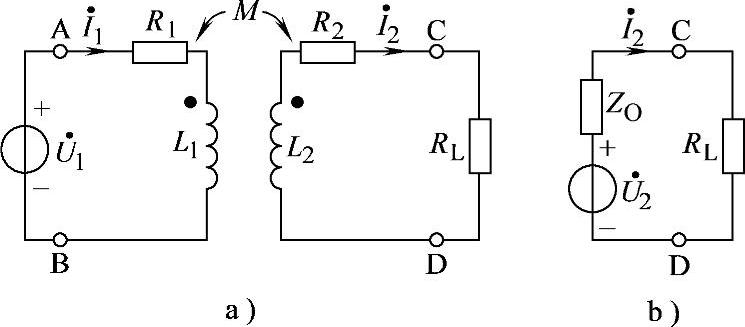
图8-62 习题8.63电路
解: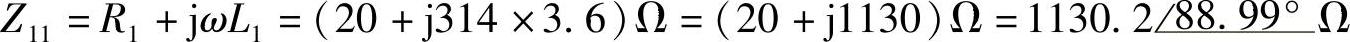
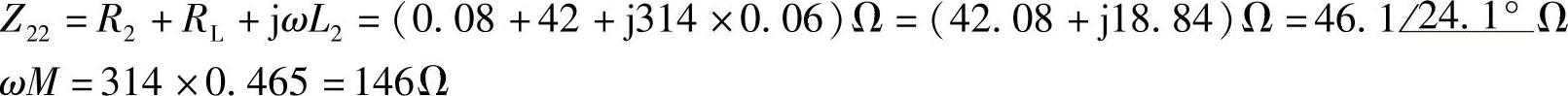
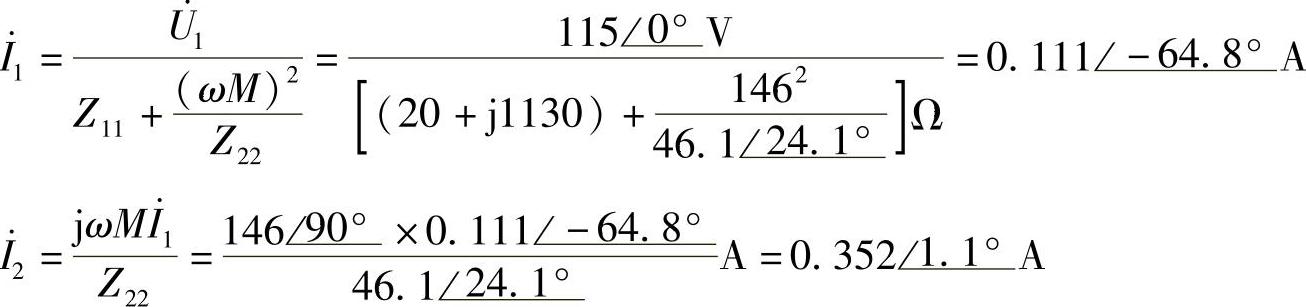
另解:本题也可用戴维南定理求解,求出CD端开路时戴维南等效电路如图8-62b所示,然后外接负载RL,求电流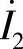 。
。
CD端开路时,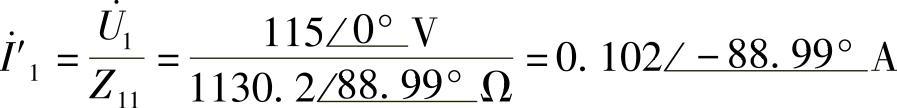
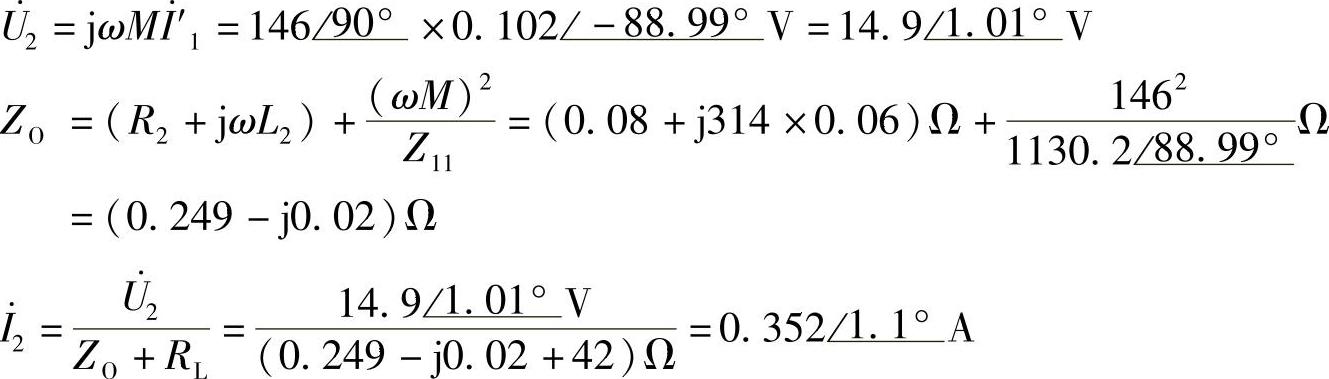
8.64 已知理想变压器一次线圈绕组N1=200匝,接在220V正弦电压上,测得二次线圈绕组端电压为22V,试求变压器变比n及二次线圈绕组匝数。
解: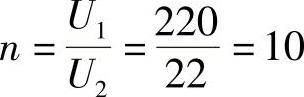
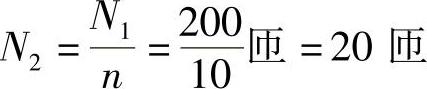
8.65 已知理想变压器电路如图8-63所示,N1=1320匝,为满足二次电压要求,试求各二次绕组匝数。
解: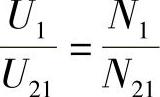 ,
,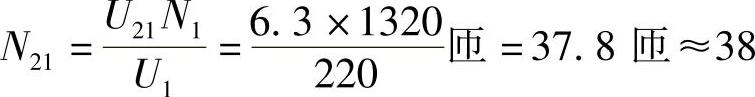 匝
匝
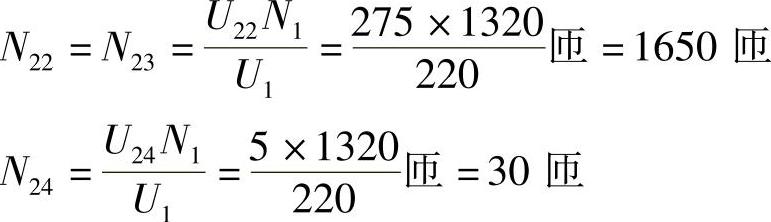
8.66 已知理想变压器N1=3000匝,N2=100匝,一次侧电流为0.22A,二次侧负载电阻为10Ω,试求一次侧输入电压和输入阻抗。
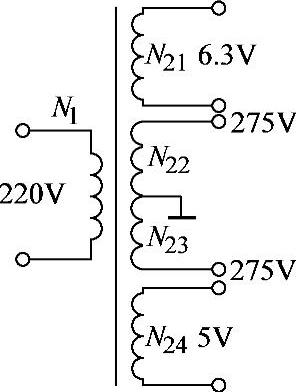
图8-63 习题8.65电路
解: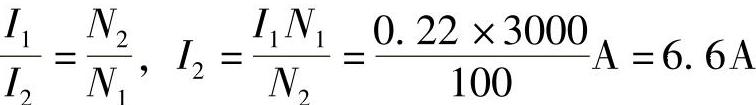
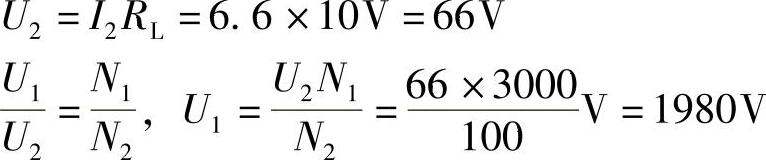
输入阻抗: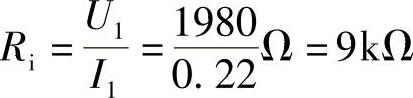
或另解: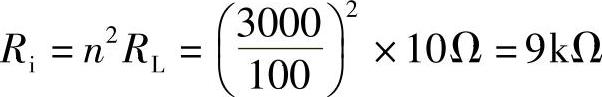
8.67 已知扩音机输出变压器,N1=300,N2=60,二次线圈原来接16Ω扬声器,现若改接8Ω扬声器,并要求一次侧输入阻抗保持不变,二次线圈匝数应改为多少?
解:一次侧输入阻抗: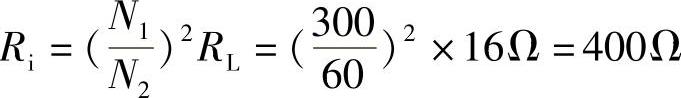
现接R′L=8Ω,则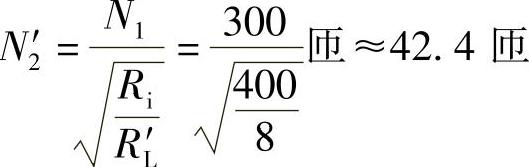 ,取N2′=43匝
,取N2′=43匝
8.68 已知收音机输出变压器变比n=5,二次侧接8Ω扬声器,试求:(1)扬声器折合到原边的等效电阻;(2)若该输出变压器一次侧接US=9V、RS=250Ω信号源,求扬声器的输出功率;(3)若不经过输出变压器,8Ω扬声器直接接上述信号源,再求扬声器输出功率。
解:(1)RL′=n2RL=52×8Ω=200Ω
(2)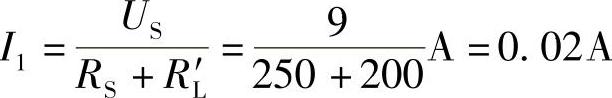
扬声器功率:PL=I21RL′=0.022×200W=0.08W
或另解:I2=nI1=5×0.02A=0.1A,PL=I22RL=0.12×8W=0.08W
(3)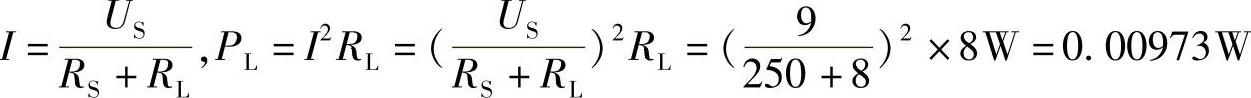
从上述计算得出,8Ω扬声器不经过输出变压器直接接信号源时,输出功率很小,效率很低。
8.69 已知电路如图8-64所示,R1=10Ω,XC=100Ω,US=100V,n=10,I1=10A,试求二次负载阻抗ZL。
解:图8-64为理想变压器电路。二次负载阻抗折合到一次侧,ZL′=n2ZL
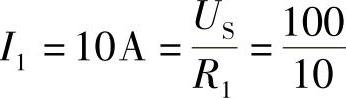 ,电流最大,表明电路已发生串联谐振。
,电流最大,表明电路已发生串联谐振。
即:ZL′-jXC=0,n2ZL=jXC
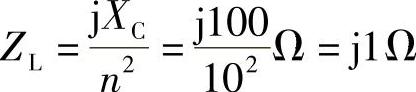
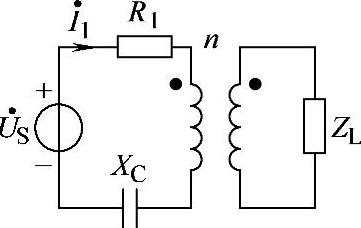
图8-64 习题8.69电路
8.70 已知理想变压器电路如图8-65所示,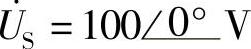 ,R1=1Ω,R2=100Ω,XL2=200Ω,n=0.1,试求
,R1=1Ω,R2=100Ω,XL2=200Ω,n=0.1,试求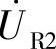 。
。
解:理想变压器一次侧阻抗:
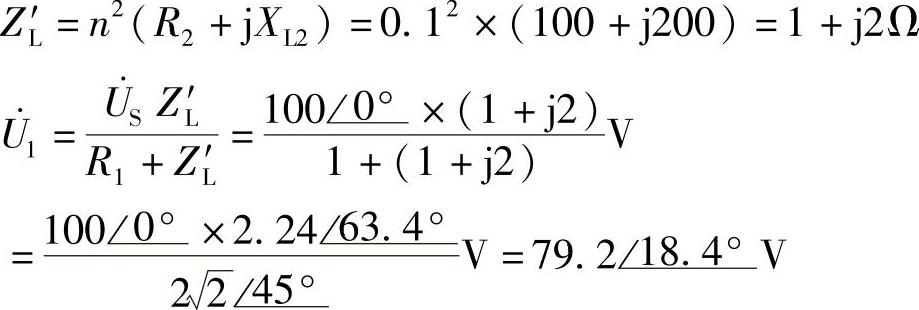
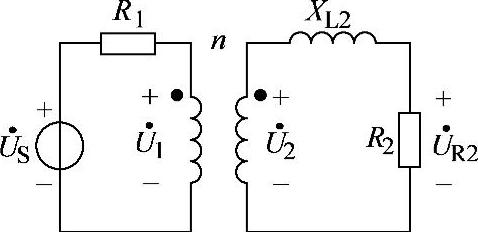
图8-65 习题8.70电路
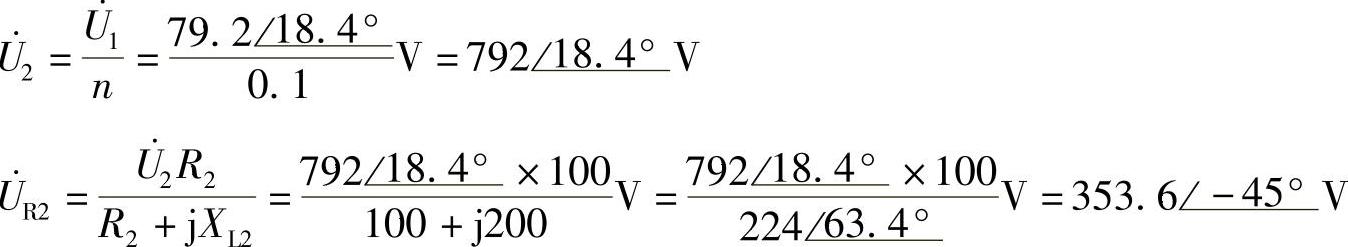
8.71 已知理想变压器电路如图8-66a所示,R1=1Ω,RL=50Ω,n=0.1,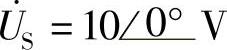 ,试求
,试求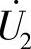 。
。
解:方法(1):利用理想变压器阻抗变换特性。
负载RL折合到一次侧:
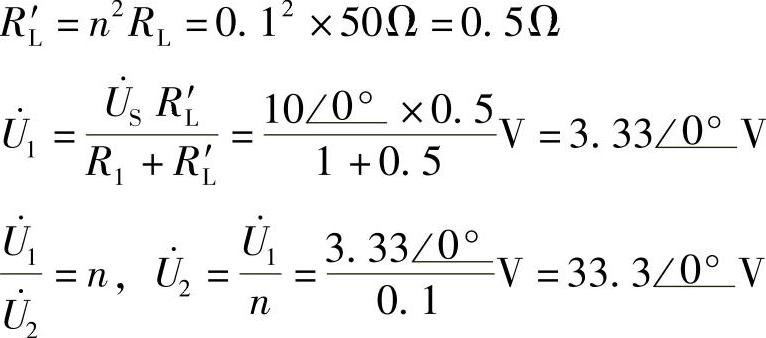
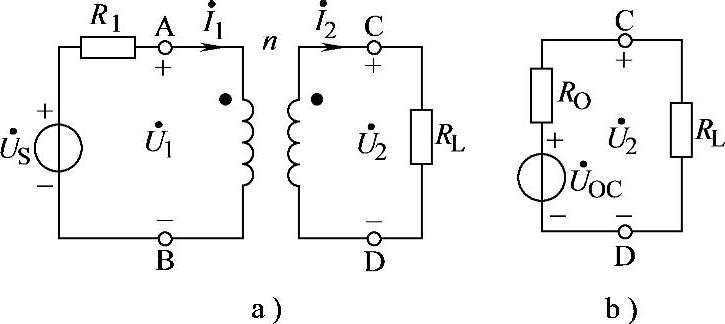
图8-66 习题8.71电路
方法(2):应用戴维南定理。
断开二次负载RL,则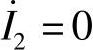 ,
,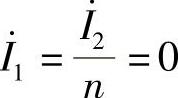 (注意:按图8-66a电路中
(注意:按图8-66a电路中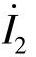 参考方向,
参考方向,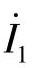 和
和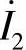 比例式中无负号),
比例式中无负号),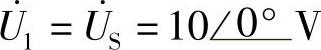 ,
,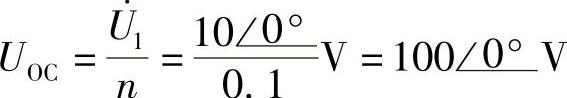
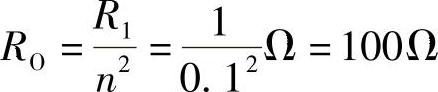 ,画出CD端戴维南等效电路如图8-66b所示。
,画出CD端戴维南等效电路如图8-66b所示。
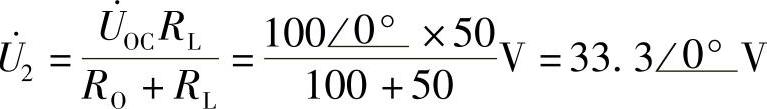
方法(3):应用网孔电流法
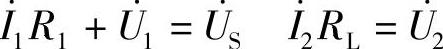
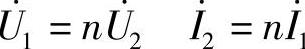 (按
(按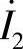 参考方向无负号)
参考方向无负号)
代入数据,联立求解得: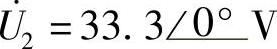
8.72 已知理想变压器电路如图8-67所示,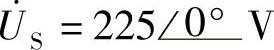 ,R1=200Ω,RL=10Ω,N1=1000匝,N2=200匝,试求:(1)负载RL上获得功率;(2)若要使RL获得最大功率,变比n应为多少?若N1不变,则N2应取多少匝?
,R1=200Ω,RL=10Ω,N1=1000匝,N2=200匝,试求:(1)负载RL上获得功率;(2)若要使RL获得最大功率,变比n应为多少?若N1不变,则N2应取多少匝?
解:(1)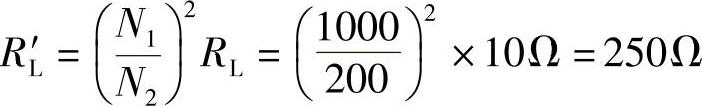
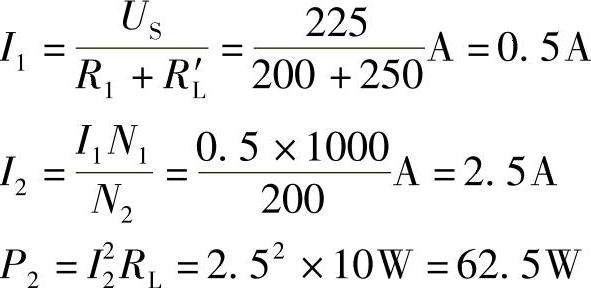
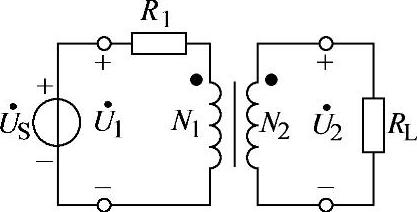
图8-67 习题8.72电路
(2)要使RL获得最大功率,应使RL′=R1=n2RL,即:
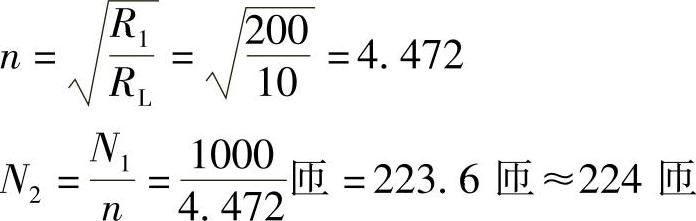
8.73 已知电路如图8-68所示,R1=10kΩ,XL1=XL2=10kΩ,XM=2kΩ,试求负载ZL获得最大功率条件。
解:从负载两端看进去的空心变压器输出阻抗:
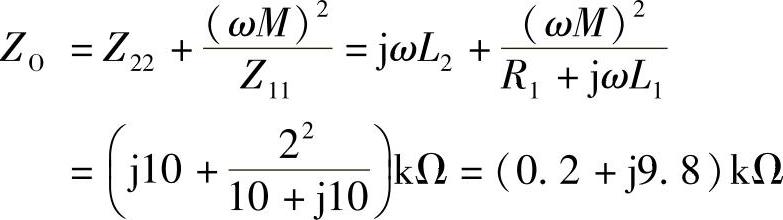
因此,ZL=ZO∗=(0.2-j9.8)kΩ时能获得最大功率。
其中ZO∗为ZO的共轭复数。
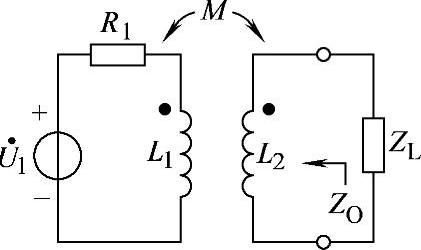
图8-68 习题8.73电路
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




