电流有效值的测量及偶函数的余弦项分析

7.1 产生非正弦周期信号的原因通常有哪些？

答：（1）电源电压为非正弦；（2）几个不同频率的正弦波共同作用于线性电路，叠加后是一个非正弦波；（3）电路中存在非线性元件。

7.2 非正弦周期奇函数和偶函数的傅里叶级数各有什么特点？

答：奇函数只含有正弦项，不含有余弦项。例如表7-1中矩形波、三角波、梯形波等。

偶函数只含有直流分量和余弦项，不含有正弦项。例如表7-1中半波整流、全波整流、矩形脉冲波等。

7.3 什么叫半波对称函数，其傅里叶级数有何特点？

答：非正弦周期波移动半个周期，与原函数后半周期波形互为镜像（即对称于横轴），即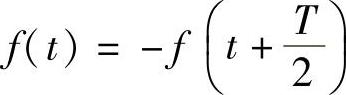，称为半波对称函数或奇谐波函数。

半波对称函数只含有奇次谐波，即k=1、3、5、…，不含有偶次谐波。例如表7-1中矩形波、三角波、梯形波等。

7.4 什么叫振幅频谱？有何特点？

答：以kω为横坐标，以各次谐波振幅为纵坐标的线段图形称为振幅频谱图。谱线的长度代表各次谐波的振幅，谱线的横坐标代表该谐波分量的角频率（或频率）。

非正弦周期波振幅频谱图具有离散性、谐波性和收敛性的特点。

7.5 数学平均值和热效应平均值有何区别？数学平均值与傅里叶级数中的常数项，直流分量有何区别？

答：数学平均值是正、负数的平均值。其定义为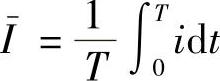：。凡是波形在一个周期内，正负面积相等的函数，其数学平均值为零。例如，正弦波、余弦波、表7-1中的矩形波、三角波、梯形波等。(www.xing528.com)

热效应平均值从电流热效应出发，无论电流为正、为负，流过耗能元件时，均要消耗一定电能，产生一定热量。其定义为：。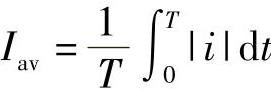

傅里叶级数中的常数项或直流分量即数学平均值。

7.6 为什么矩形波、三角波没有直流分量？

答：凡是波形在一个周期内，正负面积相等的函数，其数学平均值为零，即直流分量为零。矩形波、三角波在一个周期内，正负面积相等，因此没有直流分量。

7.7 磁电系、电磁系和电动系仪表的偏转角正比于什么因素？与测量值有何关系？

答：非正弦周期电压电流有效值、平均值的计算公式是从理论上推出的，计算一般比较繁琐。实用中，常用仪表对非正弦电压电流进行测量。

磁电系仪表的偏转角与电流成正比，只能测量直流。与整流器配合时，也可测量交流，此时其偏转角正比于电流平均值。因此，测量平均值时，应选用磁电系仪表（表头上有磁电系符号：）。

电磁系和电动系仪表的偏转角正比于电流的平方，其测量结果是电流的有效值。因此，测量有效值时，应选用电磁系（符号：）和电动系（符号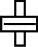：）仪表。

7.8 非正弦周期电流电路的功率因数与正弦交流电路的功率因数有何区别？

答：正弦交流电路的功率因数代表其电压与电流间相位差的余弦。

非正弦周期电流电路的功率因数并不代表非正弦周期电压与电流间相位差的余弦，非正弦周期电压与电流间无法比较和衡量相位差（不同频率正弦量相位差不是常数，不能比较），非正弦周期电流电路的功率因数仅代表了非正弦周期电流电路有功功率与视在功率的比值。