【例7-1】已知某电压波如图7-1所示,试将其分解为傅里叶级数,并求其直流分量、基波和2次谐波。
解:表7-1中无此非正弦周期波,但可将该波看作为表7-1中三角波与直流分量10V电压的叠加,因此
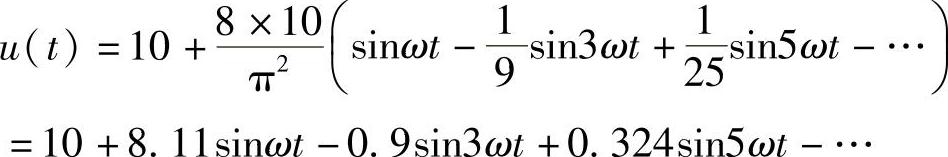
其中直流分量为10V,基波为8.11sinωt。无2次谐波分量。
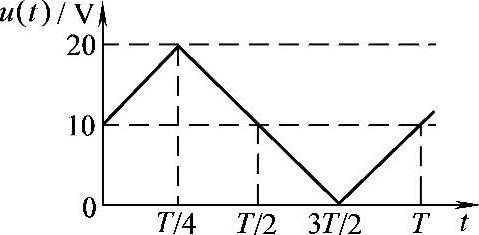
图7-1 例7-1波形图
【例7-2】试求图7-2中非正弦周期电压的直流分量和平均值。

图7-2 例7-2波形
解:直流分量是非正弦周期性函数傅里叶级数中的常数项或数学平均值,可按公式A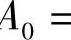
 计算。函数波形简单时,可直接用观察法、削峰填谷求解。平均值可分为数学平均值和热效应平均值,数学平均值即常数项,热效应平均值是考虑电流热效应后的平均值,应按公式
计算。函数波形简单时,可直接用观察法、削峰填谷求解。平均值可分为数学平均值和热效应平均值,数学平均值即常数项,热效应平均值是考虑电流热效应后的平均值,应按公式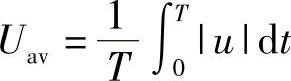 计算。
计算。
(1)u1的直流分量与平均值相等: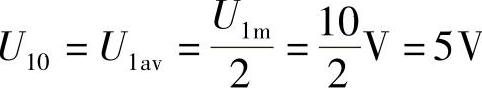 。
。
(2)因u2在一个周期内正负面积相等,其直流分量为0,即U20=0。
u2的平均值:U2av=U2m=10V
(3)直流分量:U30=0;平均值: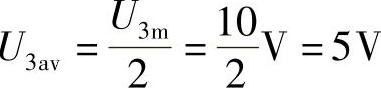
(4)u4的直流分量与平均值相等:U40=U4av=10V
【例7-3】已知电路如图7-3所示,uS(t)为表7-1中的全波整流电压,USm=12V,基波频率f=50Hz,R=1kΩ,L=2H,C=20μF,试求精确到4次谐波时的i(t)和uR(t),并计算其有效值。
解:查表7-1,全波整流电压傅里叶级数为
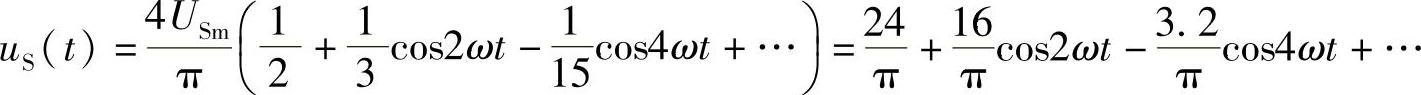
精确到4次谐波时,uS(t)包含三种成分:直流分量、2次谐波和4次谐波,现分别计算如下:
(1)直流分量单独作用,电感相当于短路,电容相当于开路。
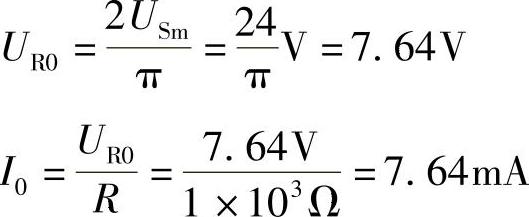
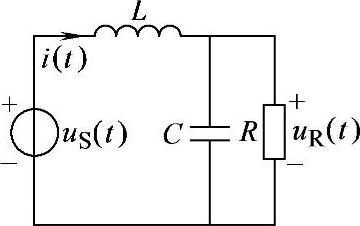
图7-3 例7-3电路
(2)二次谐波单独作用:(https://www.xing528.com)
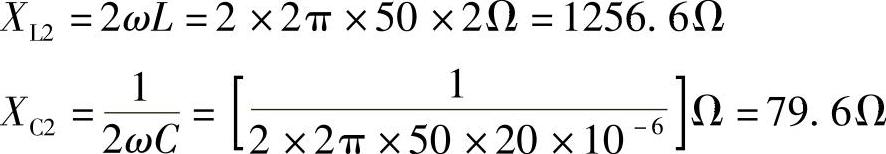
电阻电容并联支路复阻抗:
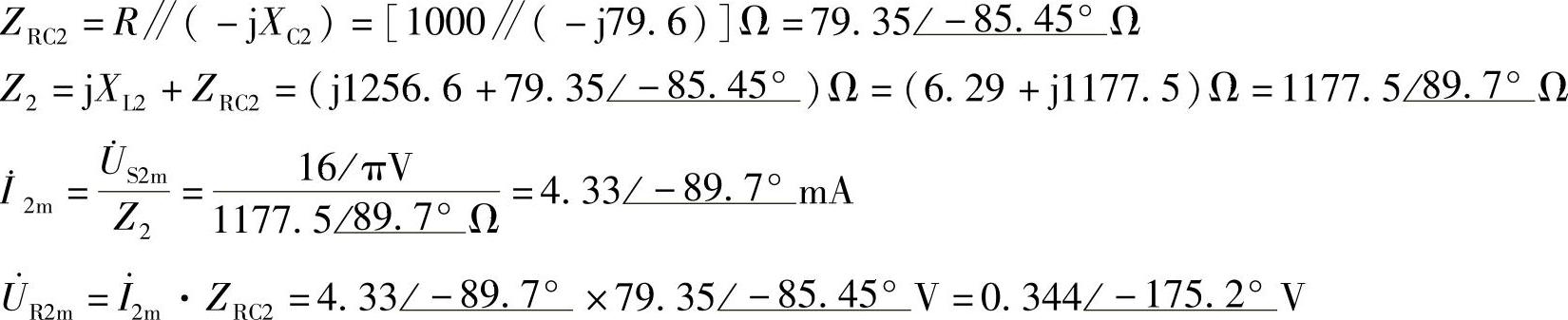
因此,i2=4.33cos(2ωt-89.7°)mA
uR2=0.344cos(2ωt-175.2°)V
(3)4次谐波单独作用:
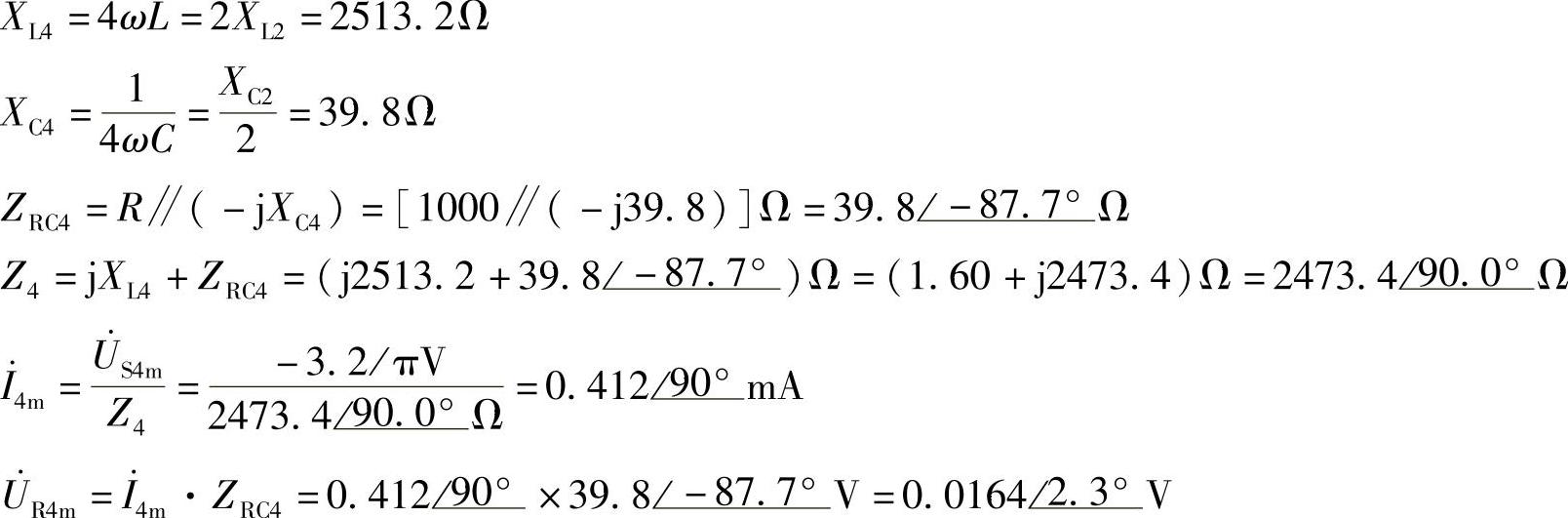
因此,i4=0.412cos(4ωt+90°)mA
uR4=0.0164cos(4ωt+2.3°)V
(4)叠加:
i(t)=I0+i2+i4=[7.64+4.33cos(2ωt-89.7°)+0.412cos(4ωt+90°)]mA
uR(t)=UR0+uR2+uR4=[7.64+0.344(2ωt-175.2°)+0.0164cos(4ωt+2.3°)]V
(5)计算有效值:
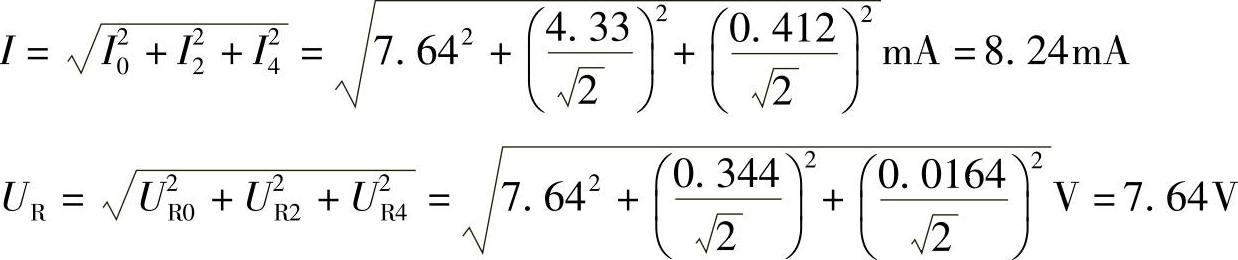
本例电路的作用将在电子技术课程LC滤波电路中详述,在此不妨提前简要说明一下。全波整流后的输入电压uS(t)中,2次谐波和4次谐波分量分别为直流分量的66.7%和13.3%,经过LC滤波后,加到负载R上电压uR(t)中的2次谐波和4次谐波分量分别只有直流分量的0.344/7.64=4.5%和0.0164/7.64=0.21%。因此,相对于直流分量,交流脉动成分已可忽略不计,uR可看做直流电压。
【例7-4】已知某二端网络两端电压u=[100+80sinωt+50sin(3ωt+60°)+20sin(5ωt+30°)]V,电流i=[1.2sin(ωt-40°)+0.8sin(3ωt+20°)+0.4sin(5ωt-30°)]A,试求其有功功率和功率因数。
解:各次谐波有功功率:
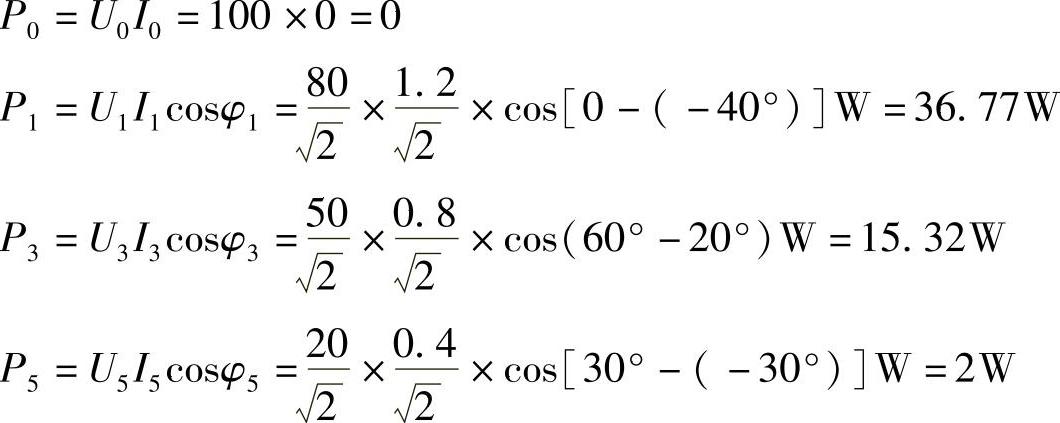
总有功功率:P=P0+P1+P3+P5=(0+36.77+15.32+2)W=54.1W
电压有效值: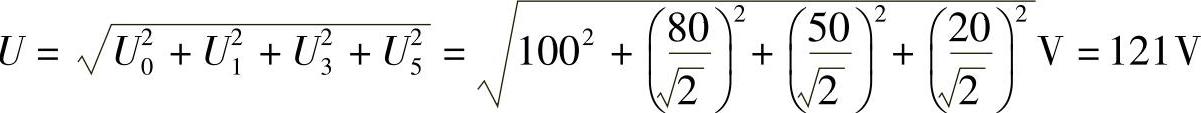
电流有效值: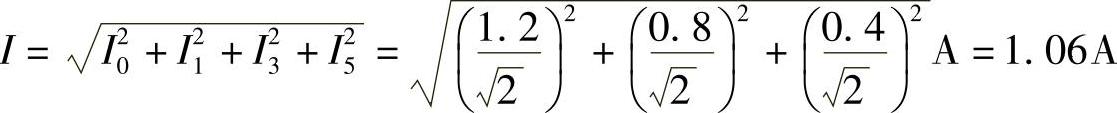
视在功率:S=UI=121×1.06VA=128.26VA
功率因数: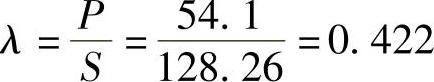
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




