4.1 已知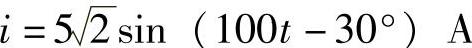 ,试求:
,试求:
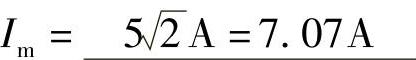 ;
;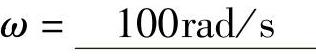 ;f=15.9Hz;φ=-30°。
;f=15.9Hz;φ=-30°。
4.2 已知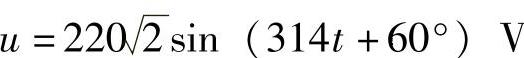 ,试求:
,试求:
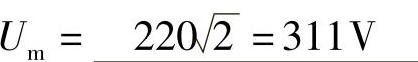 ;
;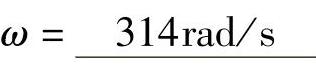 ;f=50Hz;φ=60°。
;f=50Hz;φ=60°。
4.3 已知正弦函数波形如图4-23所示,试求其初相位角。

图4-23 课堂练习题4.3波形图
4.4 已知 ,试写出iba表达式。
,试写出iba表达式。
解: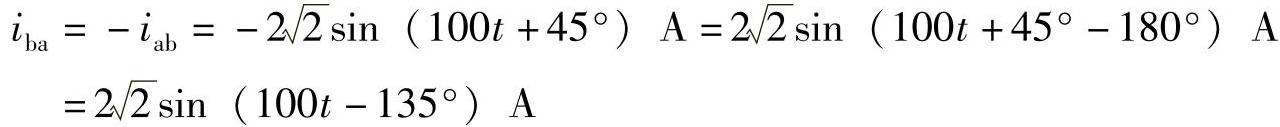
4.5 已知正弦电流如图4-24所示,若将纵坐标左移或右移30°,试分别求其初相位。
解:i坐标左移30°,φ=60°-30°=30°
i坐标右移30°,φ=60°+30°=90°
4.6 已知i1=2sin(314t+200°)A,i2=2sin(314t-200°)A,试按|φ|≤180°,写出其规范表达式。
解:正弦量表达式初相位角要求|φ|≤180°,若其超出,应予换算。因此:
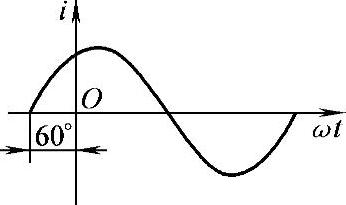
图4-24 课堂练习题 4.5 波形
i1=2sin(314t+200°)A=2sin(314t+200°-360°)A
=2sin(314t-160°)A
i2=2sin(314t-200°)A=2sin(314t-200°+360°)A=2sin(314t+160°)A
4.7 已知u=120sin(314t-20°)V,i=2sin(314t-60°)A,试求其相位差角,并说明它们之间的相位关系。
解:相位差角:φ=φu-φi=(-20°)-(-60°)=40°
相位关系:u越前i40°,或i滞后u40°。
4.8 试求课堂练习题4.6中两个电流之间的相位差角,并说明它们的相位关系。
解:相位差角:φ=φi1-φi2=(-160°)-(160°)=-320°→-320°+360°=40°
相位关系:i1越前i240°,或i2滞后i140°。
4.9 有一个电容器,耐压为250V,问能否接在民用电压220V的电源上?
解:民用电压220V为有效值,其幅值2202V=311V,已超出该电容器耐压,因此不能接在电压为220V的电源上。
4.10 已知某正弦电压平均值为100V,试求其幅值和有效值。
解: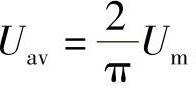 ,
,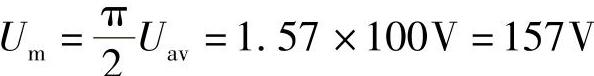
有效值: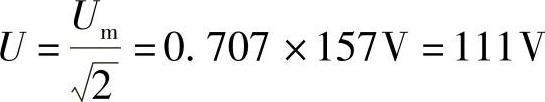
4.11 试将下列正弦相量极坐标形式写成直角坐标形式。
(1) ;(2)
;(2) ;(3)
;(3) ;(4)
;(4)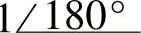 ;
;
(5)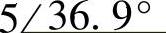 ;(6)
;(6)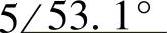 ;(7)
;(7)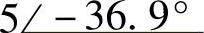 ;(8)
;(8) ;
;
(9)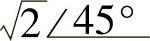 ;(10)
;(10)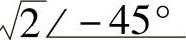 ;(11)
;(11)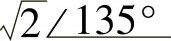 ;(12)
;(12)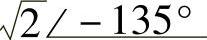 ;
;
解:(1) ;(2)
;(2)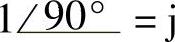 ;(3)
;(3)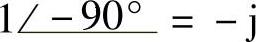 ;(4)
;(4) ;
;
(5)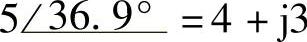 ;(6)
;(6)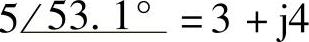 ;
;
(7)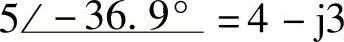 ;(8)
;(8)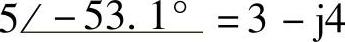 ;
;
(9)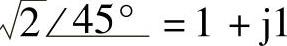 ;(10)
;(10)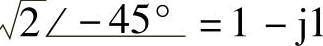 ;
;
(11)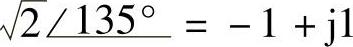 ;(12)
;(12)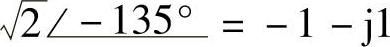 ;
;
4.12 试将下列正弦相量直角坐标形式写成极坐标形式。
(1)2;(2)2j;(3)-2j;(4)-2;
(5)-8+j6;(6)-6+j8;(7)-8-j6;(8)-6-j8;
(9)2+j2;(10)2-j2;(11)-10+j10;(12)-10-j10;
解:(1) ;(2)
;(2)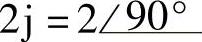 ;(3)
;(3)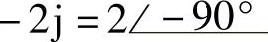 ;(4)
;(4)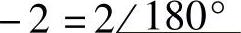 ;
;
(5)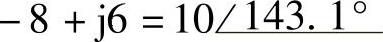 ;(6)
;(6)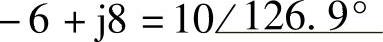 ;
;
(7)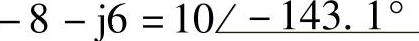 ;(8)
;(8)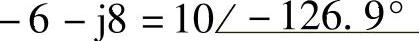 ;
;
(9)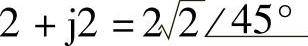 ;(10)
;(10)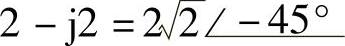 ;
;
(11)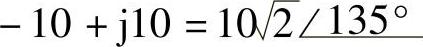 ;(12)
;(12)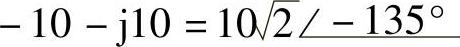 ;
;
4.13 已知正弦量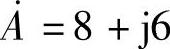 ,
,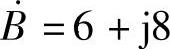 ,试求:
,试求:
(1)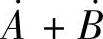 ;(2)
;(2)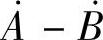 ;(3)
;(3)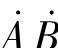 ;(4)
;(4)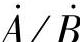 。
。
解:(1)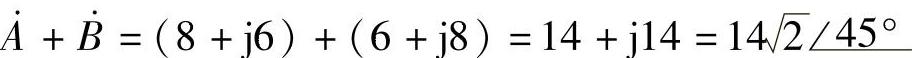
(2)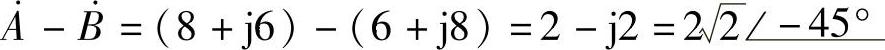
(3)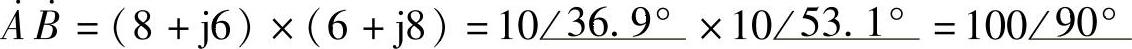
(4)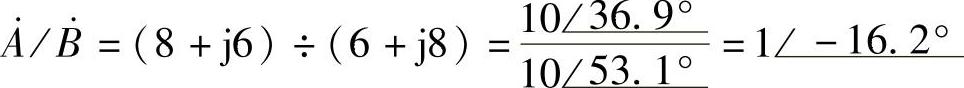
4.14 写出下列各正弦量的对应相量(极坐标和直角坐标)。
(1)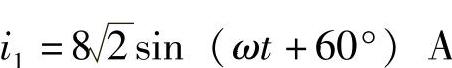 ;(2)
;(2)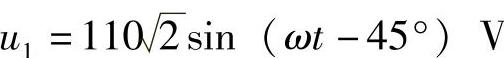
(3)i2=50sin(ωt-30°)A;(4)u2=300sin(ωt+70°)V
解:(1)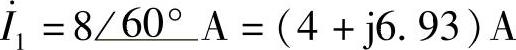 ;(2)
;(2)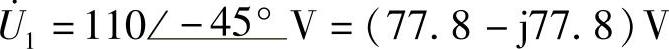
(3)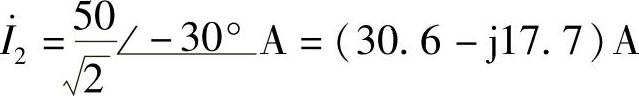 ;(4)
;(4)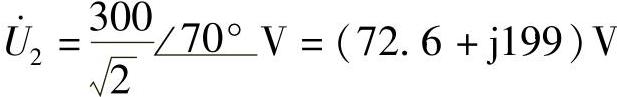
4.15 写出下列各相量对应的正弦量(角频率均为ω)。
(1)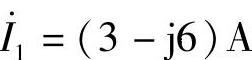 ;(2)
;(2)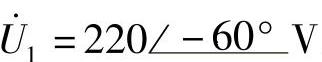 ;(3)
;(3)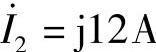 ;(4)
;(4)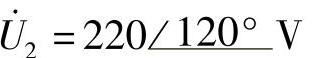
解:(1)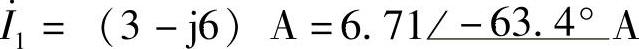 ,
,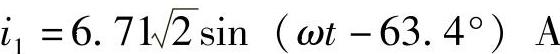
(2)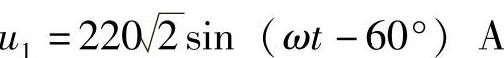
(3)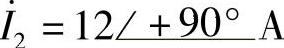 ,
,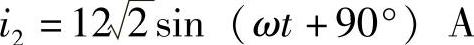
(4)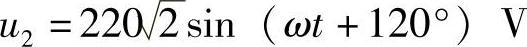
4.16 已知电阻R=25Ω,两端电压u=12.5sin(314t-60°)V,试求电阻中电流i,并画出电流电压相量图。
解: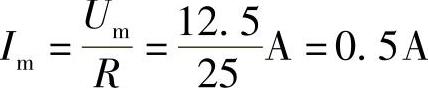
i=0.5sin(314t-60°)A
画出相量图如图4-25所示。
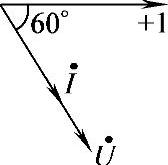
图4-25 课堂练习题4.16相量图
4.17 已知10Ω电阻上通过的电流i=5sin(314t+30°)A,试求电阻两端电压有效值,写出电压u正弦表达式。
解: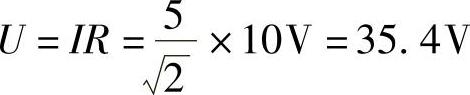
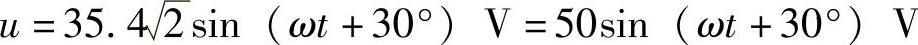 (https://www.xing528.com)
(https://www.xing528.com)
4.18 已知一线圈通过50Hz电流时,其感抗为10Ω,试求电源频率为10kHz时其感抗为多少?
解: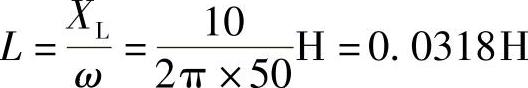
电源频率10kHz时,感抗:XL=2πfL=2π×10×103×0.0318Ω=2kΩ
4.19 已知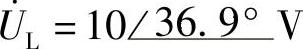 ,
,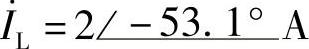 ,f=50Hz,试求XL和L。
,f=50Hz,试求XL和L。
解: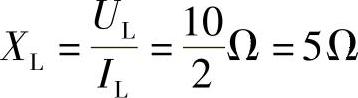
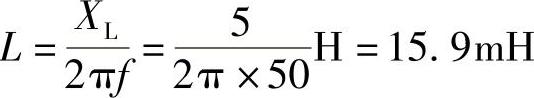
4.20 已知电感L=0.8H,uL=160sin100tV,iL与uL为关联参考方向,试求iL,并画出相量图。
解:XL=ωL=100×0.8Ω=80Ω,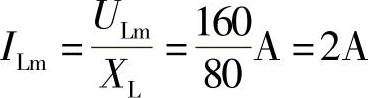
因电感中电流滞后电感两端电压90°,因此:
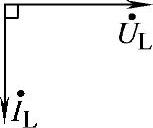
图4-26 课堂练习题4.20相量图
i=2sin(100t-90°)A
另解: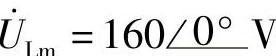 ,
,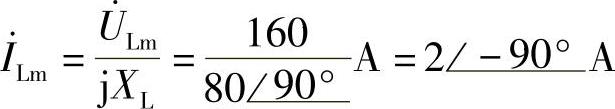 ,i=2sin(100t-90°)A
,i=2sin(100t-90°)A
画出相量图如图4-26所示。
4.21 将一个100μF的电容先后接在f=50Hz和f=500Hz,电压为220V的电源上,试分别计算上述两种情况下的容抗XL及通过电容的电流有效值。
解:f=50Hz,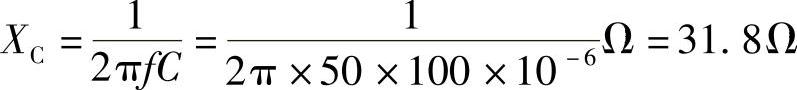 ,
,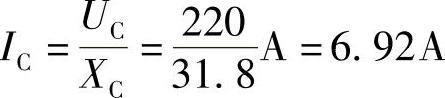
f=500Hz,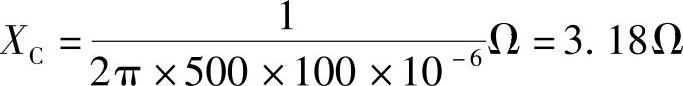 ,
,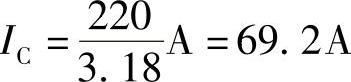
4.22 已知C=20μF,uC=600sin(314t-60°)V,试求iC(与uC关联参考方向),并画出相量图。
解: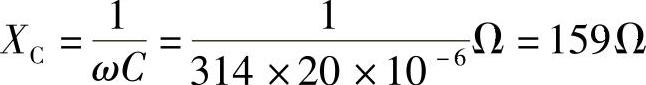 ,
,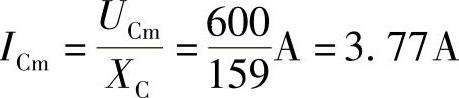
iC越前uC90°,因此
iC=3.77sin(314t-60°+90°)A=3.77sin(314t+30°)A
画出相量图如图4-27所示。
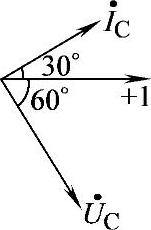
图4-27 课堂练习题 4.22 相量图
4.23 已知RLC串联正弦交流电路如图4-5所示,试判断下列电压、阻抗和阻抗角表达式的正误。
(1)U=UR+UL+UC (×) (2)u=uR+uL+uC (√)
(3)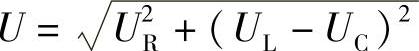 (√) (4)
(√) (4)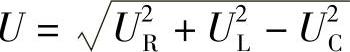 (×)
(×)
(5) (√) (6)Z=R+XL+XC (×)
(√) (6)Z=R+XL+XC (×)
(7)Z=R+XL-XC(×) (8) Z=R+j(XL-XC) (√)
(9)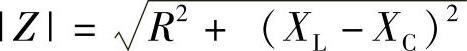 (√) (10)
(√) (10)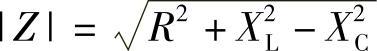 (×)
(×)
(11)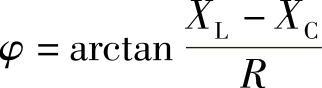 (√) (12)
(√) (12)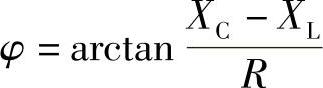 (×)
(×)
(13)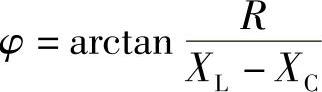 (×) (14)
(×) (14)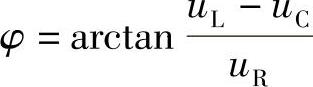 (×)
(×)
(15)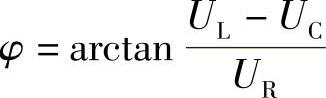 (√) (16)
(√) (16)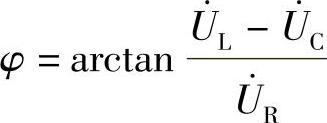 (×)
(×)
4.24 对于图4-5电路,试判断下列有关电压、特性和阻抗角说法的正误。
(1)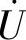 一定越前
一定越前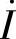 (×) (2)感性电路
(×) (2)感性电路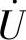 一定越前
一定越前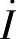 (√)
(√)
(3)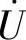 一定滞后
一定滞后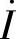 (×) (4)容性电路
(×) (4)容性电路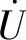 一定滞后
一定滞后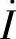 (√)
(√)
(5)若电路呈感性,则XL>XC (√) (6)若L>C,则电路呈感性 (×)
(7)若电路呈容性,则XL<XC (√) (8)若L<C,则电路呈容性 (×)
(9)若电路呈阻性,则XL=XC (√) (10)若阻抗角φ=0,则电路呈阻性 (√)
(11)若阻抗角φ>0,则电路呈容性 (×) (12)若阻抗角φ<0,则电路呈感性 (×)
(13)阻抗角φ=φi-φu (×) (14)阻抗角φ=φu-φi (√)
(15)-180°≤φ≤180° (×) (16)-90°≤φ≤90° (√)
说明:电路呈感性容性,应比较XL与XC,而不是L与C,L与C单位不同,不能比较。
4.25 已知下列电路元件参数,试求电路阻抗角。
(1)R=10Ω,XL=6Ω;(2)R=5Ω,XC=4Ω;(3)R=10Ω,XL=6Ω,XC=4Ω;
解:阻抗角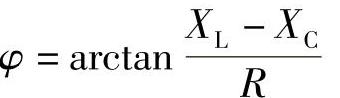
(1)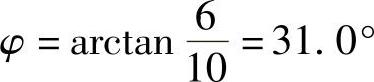 ;(2)
;(2)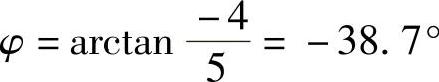 ;(3)
;(3)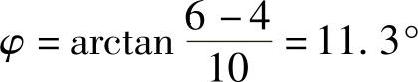
4.26 已知u(t)、i(t)波形如图4-28a、b所示,试求:
(1)f=30Hz;T=0.0333s;φu=-45°;φi=30°;U=7.07V;I=4.24A;
正弦表达式:u=10sin(60πt-45°)V;i=6sin(60πt+30°)A;
电压电流相位关系:u滞后i75°;该网络呈容性;
网络复阻抗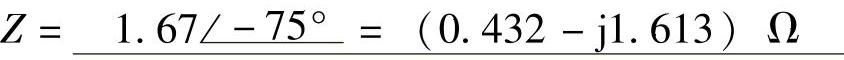 ;阻抗模:|Z|=1.67Ω;阻抗角:φ=-75°;
;阻抗模:|Z|=1.67Ω;阻抗角:φ=-75°;
复阻抗参数:R=0.432Ω;L(或C)=3289μF;
(2)f=50Hz;T=0.02s;φu=60°;φi=-15°;U=9.90V;I=14.1A;
正弦表达式:u=14sin(100πt+60°)V;i=20sin(100πt-15°)A;
电压电流相位关系:u越前i75°;该网络呈感性;
网络复阻抗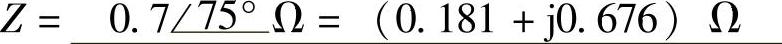 ;阻抗模:|Z|=0.7Ω;阻抗角:φ=75°。
;阻抗模:|Z|=0.7Ω;阻抗角:φ=75°。
复阻抗参数:R=0.181Ω;L(或C)=2.15mH;
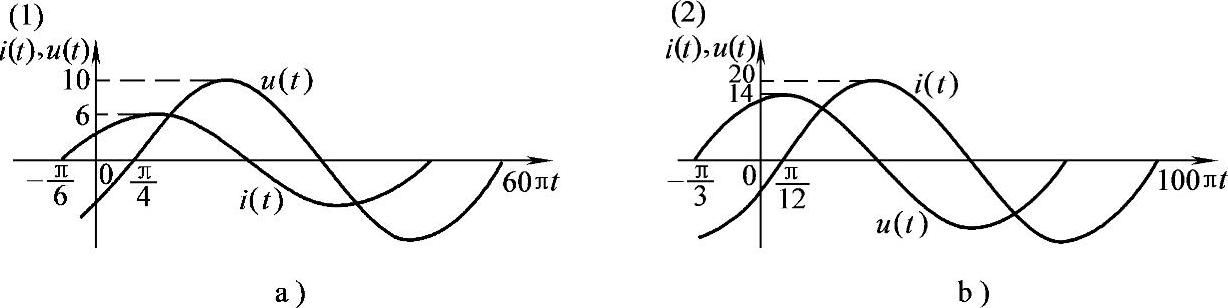
图4-28 课堂练习题4.26波形图
4.27 已知某无源二端网络端口电压电流u(t)、i(t)波形如图4-28a、b所示,试填空:
(1)有功功率:P=7.76W;无功功率:Q=-29var;
视在功率:S=30.0VA;功率因数:cosφ=0.259。
(2)有功功率:P=36.2W;无功功率:Q=135.2var;
视在功率:S=140VA;功率因数:cosφ=0.259。
4.28 已知某正弦交流电路,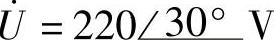 ,
, ,试求Z、R、X、P、Q、S和λ。
,试求Z、R、X、P、Q、S和λ。
解: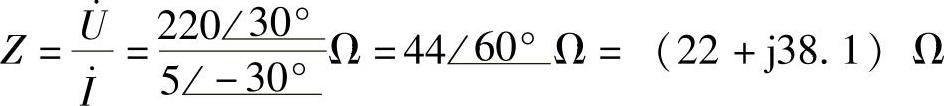
复阻抗Z实部为电阻,虚部为感抗,因此:R=22Ω,XL=38.1Ω
P=I2R=52×22W=550W
Q=I2XL=52×38.1var=952.5var
S=UI=5×220VA=1100VA
λ=cos(φu-φi)=cos[30°-(-30°)]=cos60°=0.5
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




