4.1 写出正弦电流表达式,并指出其中的三要素。
答:正弦电流表达式:i(t)=Imsin(ωt+φ)
三要素:幅值Im、角频率ω和初相位φ。
4.2 什么叫角频率ω?与频率f有何关系?ω的单位是什么?
答:角频率ω表示在单位时间内正弦量所经历的电角度。单位为弧度/秒(rad/s)。
与频率的关系:ω=2πf
4.3 我国使用的正弦交流电频率、周期和角频率是多少?
答:我国电厂发出的正弦交流电频率,称为“工频”。
f=50Hz,T=0.02s,ω=314rad/s。
4.4 什么叫相位和初相位?初相位角的大小有否要求?
答:正弦量某一时刻的电角度称为相位角,简称相位。相位角=(ωt+φ),是时间t的函数。
t=0时刻的相位称为初相位。
初相位角要求:|φ|≤180°。
4.5 为什么只有同频率的正弦量才能比较相位差?
答:两个同频率正弦量之间的相位差即为其初相位之差,是一个常数,与ωt无关。而两个不同频率正弦量之间的相位差,不是一个常数,在不断变化,与ωt有关。就像两个人在环形运动场内同向长跑,如果速度相等,那么他们之间的距离始终不变,等于他们之间的初始距离。但若他们的速度不相等,那么他们之间的距离就在不断变化。因此,两个不同频率的正弦量一般不比较相位。
4.6 比较两个正弦量之间的相位差时,什么叫越前、滞后、同相、正交和反相?
答:设两个同频率正弦量u和i的初相位分别为φu和φi。若φ=φu-φi>0,则称u越前i(或i滞后u);若φ=φu-φi<0,则称u滞后i(或i越前u);若φ=φu-φi=±90°,则称u与i正交;若φ=φu-φi=0,则称u与i同相;若φ=φu-φi=±180°,则称u与i反相,如图4-1所示。
4.7 电流有效值是根据什么定义的?写出其表达式。
答:电流有效值是根据电流热效应确定的。
有效值定义:若交流电流i通过电阻R在一个周期内所产生的热量与直流电流I在同一条件下所产生的热量相等,则这个直流电流I的数值称为交流电流i的有效值。
电流有效值表达式: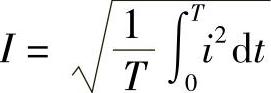
4.8 正弦电流有效值与幅值之间有何关系?非正弦电流有效值与幅值之间是否也有此关系?
答:对于正弦交流电流电压,其幅值与有效值之间有着固定的倍率关系,即: 、
、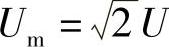 。
。
对于非正弦交流电流电压,则幅值与有效值之间均无上述2倍关系。(注:还有一种在电子技术中出现的全波整流电流电压也适用)
4.9 写出电流平均值表达式。与数学中的平均值概念有何区别?正弦电流的平均值与幅值有何关系?
答: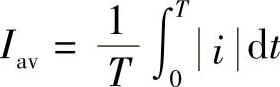
数学中的平均值是在一个周期内求和并在一个周期内平均,即 。若按此定义求平均值,那么正弦函数和对称于横轴的其他函数其平均值恒为零。因此,在电工中,平均值的概念仍含有电流热效应的内涵,即不论电流正负,均会使耗能元件发热。电工中电流平均值积分时应加绝对值符号。
。若按此定义求平均值,那么正弦函数和对称于横轴的其他函数其平均值恒为零。因此,在电工中,平均值的概念仍含有电流热效应的内涵,即不论电流正负,均会使耗能元件发热。电工中电流平均值积分时应加绝对值符号。
对于正弦交流电流: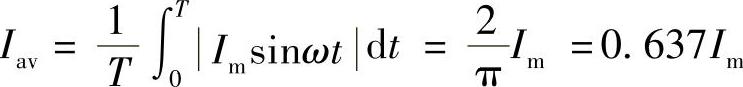
4.10 为什么要用相量表示正弦量?
答:用相量和复数表示正弦量,主要是借助其运算方法,便于解决正弦量之间的加减乘除问题。而且,当两个同频率的正弦相量置于同一复平面上时,可一目了然地比较它们的大小(长度)和相位关系(初相位角、越前滞后)。
4.11 正弦相量与复数有否区别?
答:正弦相量是时间t的函数;复数是一个数,不是时间t的函数;复数与正弦相量是两个完全不同的数学概念。为表示正弦相量与复数的区别,在正弦相量上加“·”,以示与复数和有效值的区别。
正弦相量虽然是时间t的函数,但仅表示了正弦量三要素中的二个要素,未表达出其角频率要素。用相量或复数表示正弦量,仅是表示而已。主要是借助其运算方法,便于解决正弦量之间的加减乘除问题。
4.12 如何用相量进行加减乘除运算?
答:(1)相量加减法:化成直角坐标形式(即复数形式),实部加(减)实部、虚部加(减)虚部,然后再化成极坐标形式。
(2)相量乘除法:化成极坐标形式,然后模相乘(除),幅角相加(减)。
4.13 试归纳小结纯电阻、纯电感和纯电容正弦交流电路电流电压关系相量关系,并画出相量图。
答:如表4-1所示。
4.14 感抗、容抗与频率有何关系?
答:感抗XL=ωL,角频率ω越高,感抗越大。对于直流电流来讲,ω=0,感抗XL也等于零。因此,电感对直流相当于短路。
容抗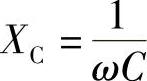 ,角频率ω越高,容抗越小。对于直流电来讲,ω=0,容抗XC→∞。因此,电容对直流相当于开路。
,角频率ω越高,容抗越小。对于直流电来讲,ω=0,容抗XC→∞。因此,电容对直流相当于开路。
4.15 试述正弦交流电路感性、容性和阻性三种情况的特点。
答:电路呈感性时,UL>UC,XL>XC,φ>0;
电路呈容性时,UL<UC,XL<XC,φ<0;
电路呈阻性时,UL=UC,XL=XC,φ=0。(https://www.xing528.com)
因此,RLC串联正弦交流电路,只需已知上述4个特点中的一个,即可得出另外3个特点。
4.16 第1、2章中推出的电路定律和分析方法在正弦交流电路中是否适用?
答:正弦交流电路引入复阻抗和复导纳后,第1、2章中推出的电路定律和分析方法均能使用。但电流电压须用相量表示,复阻抗和复导纳须用复数表示,按相量运算规则运算。
4.17 什么叫感纳、容纳、电纳和复导纳、复导纳模、导纳角?与感抗、容抗、电抗和复阻抗、复阻抗模、阻抗角有何关系?
答:(1)感纳: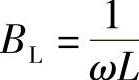 ;感抗:XL=ωL。感纳与感抗互为倒数;
;感抗:XL=ωL。感纳与感抗互为倒数;
(2)容纳:BC=ωC;容抗: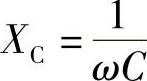 。容纳与容抗互为倒数;
。容纳与容抗互为倒数;
(3)电纳:B=BC-BL;电抗:X=XL-XC。B≠1/X。
(4)复导纳: ;
;
复阻抗: ;复导纳Y与复阻抗Z互为倒数。
;复导纳Y与复阻抗Z互为倒数。
(5)复导纳模: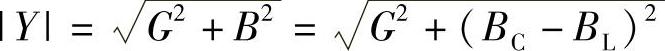 ;
;
复阻抗模:
复导纳模|Y|与复阻抗模|Z|互为倒数。
(6)导纳角: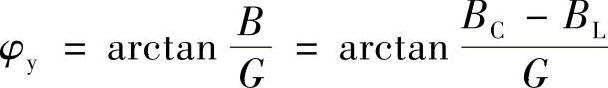 ;
;
阻抗角: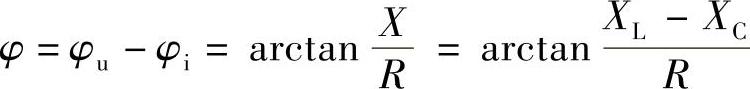 ;
;
阻抗角φ与导纳角φy的关系:φ=-φy。
4.18 导纳角与阻抗角是否相等?
答:阻抗角φ与导纳角φy的关系:φ=-φy。
4.19 怎样画正弦交流电路的相量图?
答:正弦交流电路的相量图可按下述步骤进行:
(1)先画出参考相量。
1)串联电路,流过每个元件的电流相同,因此可以电流相量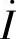 作为参考相量;若已知
作为参考相量;若已知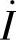 初相位φi,则按φi画出
初相位φi,则按φi画出 ;若未知
;若未知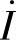 初相位φi,则一般可设φi=0画出
初相位φi,则一般可设φi=0画出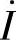 。
。
2)并联电路,每个元件两端的电压相同,因此可以电压相量 作为参考相量。若已知
作为参考相量。若已知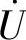 初相位φu,则按φu画出
初相位φu,则按φu画出 ;若未知
;若未知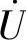 初相位φu,则一般可设φu=0画出
初相位φu,则一般可设φu=0画出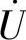 。
。
(2)根据参考相量,画出与参考相量有关的相量。
1)串联电路,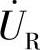 与
与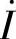 同相;
同相; 越前
越前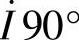 ,即
,即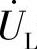 按逆时针方向旋转90°,垂直于
按逆时针方向旋转90°,垂直于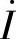 ;
;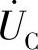 滞后
滞后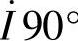 ,即
,即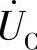 按顺时针方向旋转90°,垂直于
按顺时针方向旋转90°,垂直于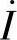 ;因此
;因此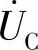 恒与
恒与 反相。
反相。
2)并联电路,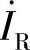 与
与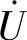 同相;
同相;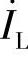 滞后
滞后 ,即
,即 按顺时针方向旋转90°,垂直于
按顺时针方向旋转90°,垂直于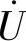 ;
; 越前
越前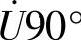 ,即
,即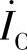 按逆时针方向旋转90°,垂直于
按逆时针方向旋转90°,垂直于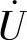 ;因此
;因此 恒与
恒与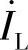 反相。
反相。
(3)在画与参考相量有关的相量时,一般可按首尾相接法依次画出。
1)串联电路,先画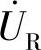 ,再画
,再画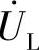 ,
,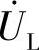 的首(相量起始端)接
的首(相量起始端)接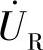 的尾(相量箭头端);
的尾(相量箭头端);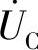 的首接
的首接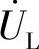 的尾。最后画总电压
的尾。最后画总电压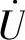 ,总电压
,总电压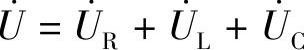 ,从
,从 的首至
的首至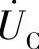 的尾即为总电压
的尾即为总电压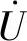 (形成一个封闭的多边形)。
(形成一个封闭的多边形)。
2)并联电路,先画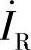 ,再画
,再画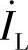 ,
, 的首(相量起始端)接
的首(相量起始端)接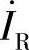 的尾(相量箭头端);
的尾(相量箭头端);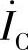 的首接
的首接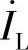 的尾。最后画总电流
的尾。最后画总电流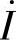 ,总电流
,总电流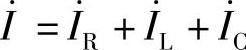 ,从
,从 的首至
的首至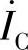 的尾即为总电流
的尾即为总电流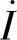 (形成一个封闭的多边形)。
(形成一个封闭的多边形)。
(4)因电流与电压属两个不同的物理量,因此电流与电压不能比较大小,即参考相量的长度可任意画,一般宜长些(相位关系更一目了然)。同一物理量的长度不能乱画(其长度具有可比性),应按理论计算值大小,按比例确定其长度(相量长度代表其大小),而总电压(或总电流)的长度是分电压(或分电流)相量相加的结果。
4.20 有功功率与瞬时功率有何关系?
答:有功功率也称为平均功率,它是瞬时功率在一个周期内的平均值,即瞬时功率中的恒定分量。
4.21 电路的有功功率,为什么只需计算电路内各个电阻的功率之和?
答:电感L与电容C为储能元件,不是耗能元件。电感的有功功率PL和电容的有功功率PC恒为0。因此,电路的有功功率与电路内储能元件无关(但U、I值与电路内储能元件还是有关的)。计算一个二端网络的有功功率时,只需要计算该网络内所有电阻的有功功率之和。
4.22 电路的无功功率,为什么只需计算电路内各储能元件的无功功率之和?
答:无功功率定义为电路中储能元件与外电路或电源之间能量交换的最大速率,与电路中的耗能元件电阻无关(但U、I值与网络内电阻元件还是有关的)。因此,计算一个二端网络的无功功率时,只需要计算网络内所有储能元件的无功功率之代数和。
4.23 P=UIcosφ中的U、I、φ各指电路中的哪个电压、电流、阻抗角?
答:U、I是电路总电压u和总电流i的有效值U和I,φ角是总电压u与总电流i的相位差角,φ=φu-φi。
4.24 什么叫视在功率?
答:视在功率定义为电气设备总的功率容量。电气设备的视在功率不仅体现在它的有功功率,还应包括它与外电路或电源交换能量的无功功率。因此能表明电气设备功率总容量的是视在功率。
4.25 画出功率三角形,功率三角形与电压三角形、电流三角形、阻抗三角形,三者有何关系?
答:功率直角三角形,如图4-11所示。功率三角形与电压三角形、电流三角形、阻抗三角形是相似三角形。
4.26 为什么要提高功率因数?如何提高功率因数?
答:提高功率因数有着很大的经济意义。一是可充分利用电源设备的功率容量。二是减少电能在传输线路中的损耗,提高输电效率。
提高功率因数的方法是在感性负载两端并联电容器。并联电容后,总电流反而减小了。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




