正弦交流电路基本原理及应用介绍

1.正弦量表达式（以正弦交流电流为例）

i（t）=I_msin（ωt+φ）

2.正弦量三要素

确定一个正弦量必须具备三个要素：幅值I_m、角频率ω和初相位φ。

（1）幅值I_m：正弦交流电流的最大值、振幅值。

（2）角频率ω：单位时间内正弦量所经历的电角度。单位：弧度/秒（rad/s）。

1）与频率的关系：ω=2πf

2）工频：我国正弦交流电频率。f=50Hz，T=0.02s，ω=314rad/s。

（3）初相位φ。

1）相位角（ωt+φ）：正弦量某一时刻的电角度，简称相位，是时间t的函数。

2）初相位φ：t=0时刻的相位角。要求初相位|φ|≤180°。

3.同频率正弦量之间的相位差

两个同频率正弦量之间的相位之差，称为相位差。φ=φ_u-φ_i

（1）越前：若φ=φ_u-φ_i＞0，则称u越前i（或i滞后u），如图4-1a所示。

（2）滞后：若φ=φ_u-φ_i＜0，则称u滞后i（或i越前u），如图4-1b所示。

（3）正交：若φ=φ_u-φ_i=±90°，则称u与i正交，如图4-1c所示。

（4）同相：若φ=φ_u-φ_i=0，则称u与i同相，如图4-1d所示。

（5）反相：若φ=φ_u-φ_i=±180°，则称u与i反相，如图4-1e所示。(www.xing528.com)

图4-1 两个同频率正弦量之间的相位关系

a）u越前i b）i越前u c）正交 d）同相 e）反相

4.有效值和平均值

（1）有效值。

1）定义：根据电流热效应确定，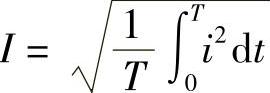

2）正弦量有效值：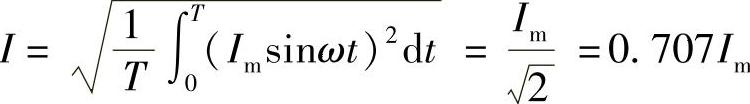

（2）平均值。

1）定义：仍与电流热效应有关，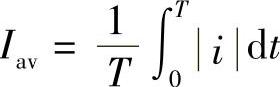

2）正弦量平均值：

5.正弦量的相量表示法

（1）极坐标形式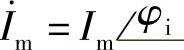：或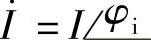

（2）直角坐标形式：。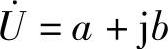

注意：正弦量是时间t的函数；复数是一个数，不是时间t的函数；复数与正弦量是两个完全不同的数学概念。用相量或复数表示正弦量，仅仅是表示而已。主要是借助其运算方法，便于解决正弦量之间的加减乘除问题。

6.相量运算

（1）相量加减法：化成直角坐标形式（即复数形式），实部加（减）实部、虚部加（减）虚部，然后再化成极坐标形式。

（2）相量乘除法：化成极坐标形式，然后模相乘（除），幅角相加（减）。