填空题解答：了解时间常数和孔径的关系

3.1 电容定义式为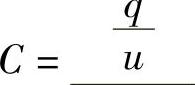。单位为法[拉]，用字母F表示。

3.2 电容元件简称电容。实际上“电容”这个名词代表双重含义，既代表电容元件，又表示电容参数。

3.3 流过电容的电流i_C与电容两端电压u_C的关系为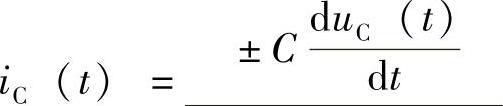（微分表达式）或（积分表达式）。式中正负号取法：若i_C和u_C参考方向一致；取正号；若相反，取负号。

3.4 电感定义式为。单位为亨[利]，用字母H表示。

3.5 流过电感的电流i_L与电感两端电压u_L的关系为（微分表达式）或（积分表达式）。式中正负号取法：若i_L和u_L参考方向一致；取正号；若相反，取负号。

3.6 电路从一种稳定状态变化到另一种稳定状态的中间过程称为电路过渡过程。

3.7 引起电路过渡过程的外因是电路换路；内因是电路中含有储能元件。

3.8 换路定律：电路在换路瞬间，电容两端电压和电感中电流不能跃变。

3.9 产生换路定律结论的原因是激励电源的功率不可能为∞。

3.10 一阶电路含有一个动态元件，可用一阶微分方程描述和求解。

3.11 零输入响应是指电路不再输入新的能量，依靠原有储能产生过渡过程。这种电路一定是储能元件放电电路，最终，储能为0。

3.12 时间常数τ反映了电路过渡过程的快慢。(www.xing528.com)

3.13 从理论上讲，过渡过程要到t→∞时结束。但实际上经过3τ～5τ，就可以认为过渡过程基本上结束了。

3.14 在零输入响应中，τ表示储能元件从初始电流或电压值按指数规律衰减到36.8%时所需的时间，3τ时已衰减到初始电流或电压值的0.05；5τ时已衰减到初始电流或电压值的0.007。

3.15 零状态响应是在电路储能元件初始储能为零状态下，由外施激励引起的响应。这种电路一定是储能元件由零开始充电，最终充至最大值。

3.16 在零状态响应中，τ表示储能元件从0开始按指数规律增大到0.632最终（最大）电流或电压值所需时间。3τ时已增大到0.95；5τ时已增大到0.993。

3.17 一阶电路全响应是一阶电路在非零初始状态下受到外施激励后产生的响应。可分解为稳态分量和暂态分量，也可分解为零输入响应和零状态响应。

3.18 在计算τ值时，R应理解为从动态元件（C或L）两端看进去的戴维南电路的等效电阻。

3.19 阶跃函数可以作为开关动作的数学模型，因此也称为开关函数。

3.20 阶跃响应可看作为电路在阶跃函数的激励下产生的零状态响应。

3.21 微分电路输入输出电压关系为，其条件为。

3.22 积分电路输入输出电压关系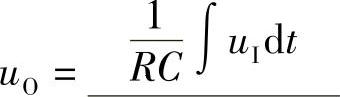为，其条件为。

3.23 RLC串联零输入响应当时，电路响应为非振荡状态；当时，电路响应为减幅振荡状态。